VectorFieldGraph2D1

Graphing a Vector Field in the Plane

Click to enlarge

This PG code shows how to graph a vector field in the plane.

• File location in OPL: FortLewis/Authoring/Templates/VectorCalc/VectorFieldGraph2D1.pg

Templates by Subject Area

PG problem file	Explanation
Problem tagging data	Problem tagging:
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "PGgraphmacros.pl", "VectorField2D.pl", ); TEXT(beginproblem()); $refreshCachedImages = 1;	Initialization: We need to include the macros file VectorField2D.pl.
Context()->variables->add(y=>"Real"); # # Create a graph canvas # $gr = init_graph(-5,-5,5,5,grid=>[10,10],axes=>[0,0],pixels=>[400,400]); $gr->lb('reset'); foreach my $j (1..4) { $gr->lb( new Label(-4.7, $j, $j,'black','center','middle')); $gr->lb( new Label(-4.7, -$j,-$j,'black','center','middle')); $gr->lb( new Label( $j,-4.7, $j,'black','center','middle')); $gr->lb( new Label( -$j,-4.7,-$j,'black','center','middle')); } $gr->lb( new Label(4.7,0.2,'x','black','center','middle')); $gr->lb( new Label(0.2,4.7,'y','black','center','middle')); 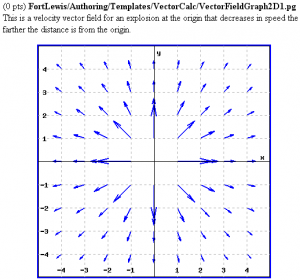VectorField2D( graphobject => $gr, Fx => Formula("x/(x^2+y^2)"), Fy => Formula("y/(x^2+y^2)"), xvar => "x", yvar => "y", xmin => -5, xmax => 5, ymin => -5, ymax => 5, xsamples => 10, ysamples => 10, vectorcolor => "blue", vectorscale => 1.5, vectorthickness => 2, xavoid=>0, yavoid=>0, );	Setup: We create a blank graph canvas and add labels to it. Then, using the VectorField2D() subroutine, we specify the formula for the vector field and its parameters. The values for xsamples and ysamples were chosen so that the tails of the vectors would be on lattice points (this routine automatically adds one to the samples values, which is usually what you want since there are 11 integers between -5 and 5 including endpoints). You can uniformly rescale the length of all the vectors in the vector field by setting vectorscale to a different value (natural length is 1). You can avoid one point with coordinates (xavoid,yavoid) where the vector field may be undefined.
Context()->texStrings; BEGIN_TEXT This is a velocity vector field for an explosion at the origin that decreases in speed the farther the distance is from the origin. $PAR $BCENTER \{ image(insertGraph($gr),width=>400,height=>400,tex_size=>700) \} $ECENTER END_TEXT Context()->normalStrings;	Main Text:
$showPartialCorrectAnswers = 1;	Answer Evaluation:
Context()->texStrings; BEGIN_SOLUTION Solution explanation goes here. END_SOLUTION Context()->normalStrings; COMMENT('MathObject version.'); ENDDOCUMENT();	Solution:

Templates by Subject Area