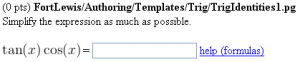
TrigIdentities1
Jump to navigation
Jump to search
This problem has been replaced with a newer version of this problem
Requiring Trig Identities be Used by Cleverly Redefining Functions
This PG code shows how to redefine a named function internally so that students must apply a trig identity and simplify their answer.
- File location in OPL: FortLewis/Authoring/Templates/Trig/TrigIdentities1.pg
- PGML location in OPL: FortLewis/Authoring/Templates/Trig/TrigIdentities1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", "answerHints.pl", ); TEXT(beginproblem()); |
Initialization: |
Context("Numeric");
Context()->functions->remove("tan");
package NewFunc;
# this next line makes the function a
# function from reals to reals
our @ISA = qw(Parser::Function::numeric);
sub tan {
shift; my $x = shift;
return CORE::exp($x*3.1415926535);
}
package main;
# Make it work on formulas as well as numbers
sub tan {Parser::Function->call('tan',@_)}
# Add the new functions to the Context
Context()->functions->add(
tan => {class =>'NewFunc', TeX =>'\tan'}, );
|
Setup:
We redefine the function whose
name is |
Context()->texStrings;
BEGIN_TEXT
Simplify the expression as much as possible.
$BR
$BR
\( \tan(x) \cos(x) \) = \{ ans_rule(20) \}
\{ AnswerFormatHelp("formulas") \}
END_TEXT
Context()->normalStrings;
|
Main Text: |
$showPartialCorrectAnswers = 1;
ANS(Formula("sin(x)")->cmp()
->withPostFilter(AnswerHints(
Compute("tan(x)*cos(x)") =>
"No credit for entering what you were given.",
))
);
|
Answer Evaluation: |
Context()->texStrings;
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |