Differential Equations Essay Style Problem
Problem with Flash Applets and Essay Style Questions
Sample Problem with WWPluggableODESystem.swf
This sample problem shows how to use the phase portrait applet together with essay-style questions.
This applet and WeBWorK problem are based upon work supported by the National Science Foundation under Grant Number DUE-0941388.
Click here to see a problem like this in action: [1]
A standard WeBWorK PG file with an embedded applet has six sections:
- A tagging and description section, that describes the problem for future users and authors,
- An initialization section, that loads required macros for the problem,
- A problem set-up section that sets variables specific to the problem,
- An Applet link section that inserts the applet and configures it, (this section is not present in WeBWorK problems without an embedded applet)
- A text section, that gives the text that is shown to the student, and
- An answer and solution section, that specifies how the answer(s) to the problem is(are) marked for correctness, and gives a solution that may be shown to the student after the problem set is complete. For the problem in this example, answers are to be graded by the instructor, after the homework set is due.
The screenshot below shows part of the problem as the student sees it:
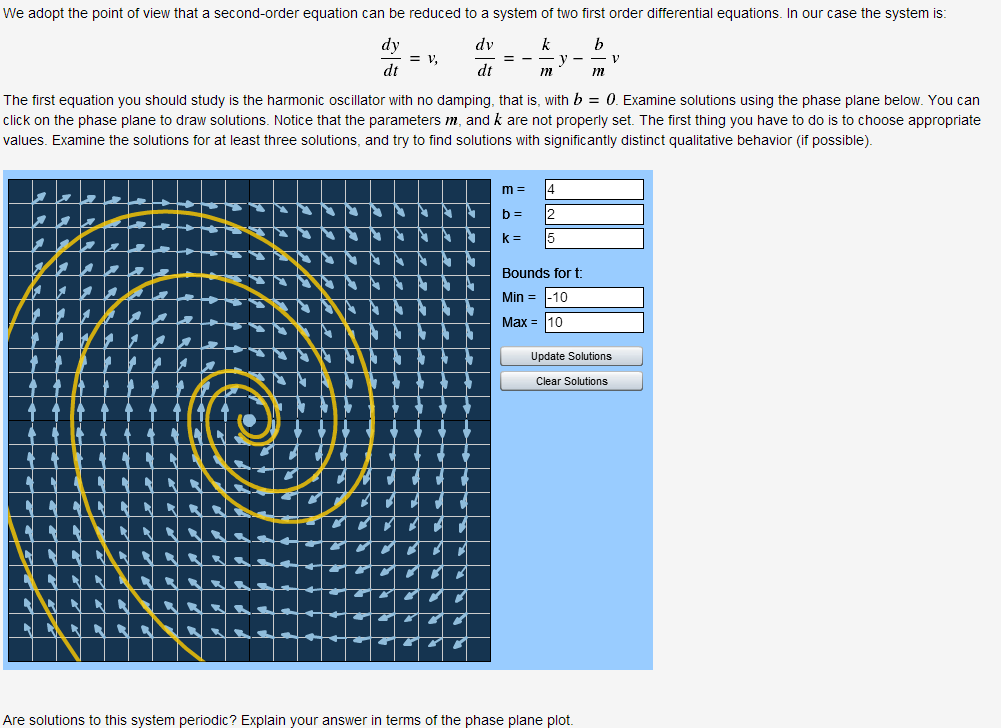
The student can select the parameters of the equation and click on the slope field to display solution curves. The appearance of the applet, as well as the system of differential equations being represented, are customizable in the problem pg file. If desirable, the student can be allowed to enter the full equations defining the system.
There are other sample problems using applets:
GraphLimit Flash Applet Sample Problem
GraphLimit Flash Applet Sample Problem 2
trigwidget Applet Sample Problem
uSub Applet Sample Problem
| PG problem file | Explanation |
|---|---|
#DESCRIPTION
## Linked Problem for Diff Eq lab
##ENDDESCRIPTION
##KEYWORDS('harmonic oscillator', 'damping')
## DBsubject('Calculus')
## DBchapter('Differential Equations')
## DBsection('The Logistic Equation')
## Date('10/25/2012')
## Author('L. Felipe Martins')
## Author('Barbara Margolius')
## Institution('Cleveland State University')
## TitleText1('Differential Equations')
## EditionText1('4')
## AuthorText1('Blanchard, Devaney, Hall')
## Chapter('2')
## Problem1('2.3')
###################################################
# This work is supported in part by the
# National Science Foundation under the
# grant DUE-0941388.
###################################################
|
This is the tagging and description section of the problem. Note that any line that begins with a "#" character is a comment for other authors who read the problem, and is not interpreted by WeBWorK. The description is provided to give a quick summary of the problem so that someone reading it later knows what it does without having to read through all of the problem code. All of the tagging information exists to allow the problem to be easily indexed. Because this is a sample problem there isn't a textbook per se, and we've used some default tagging values. There is an on-line list of current chapter and section names and a similar list of keywords. The list of keywords should be comma separated and quoted (e.g., KEYWORDS('calculus','derivatives')). |
DOCUMENT();
loadMacros(
"PGanswermacros.pl",
"PGstandard.pl",
"AppletObjects.pl",
"MathObjects.pl",
"PGasu.pl",
"PGessaymacros.pl",
);
|
This is the initialization section of the problem. The first executed line of the problem must be the
The |
# Print problem number and point value (weight) for the problem
TEXT(beginproblem());
# Show which answers are correct and which ones are incorrect
$showPartialCorrectAnswers = 1;
##############################################################
#
# Setup
#
#
Context("Numeric");
@params_array = (
[2,5,2,3],
[3,5,3,3],
[5,5,4,3],
[2,6,3,5],
[3,6,3,5],
[5,6,3,5],
[5,4,4,2],
[5,5,4,2],
[5,6,4,2],
[5,4,4,2]);
SRAND($psvn);
$choice = random(0,9,1);
$m = $params_array[$choice][0];
$k = $params_array[$choice][1];
$b = $params_array[$choice][2];
$alpha = $params_array[$choice][3];
|
This is the problem set-up section of the problem. Each version of the problem uses a different set of parameters for the system of differential equations. Notice that, since WeBWorK does not do any grading for this problem, the setup is quite simple. Also note the use of $psvn, which allows to use the same random seed for a sequence of problems. |
##############################################################
#
# Applet object definition
#
#
$appletName = "WWPluggableODESystem";
$applet = FlashApplet(
codebase => findAppletCodebase("$appletName.swf"),
appletName => $appletName,
appletId => $appletName,
setStateAlias => 'setXML',
getStateAlias => 'getXML',
setConfigAlias => 'setConfig',
maxInitializationAttempts => 10,
#answerBoxAlias => 'answerBox',
height => '500',
width => '650',
bgcolor => '#99CCFF',
debugMode => 0,
submitActionScript => '',
);
##############################################################
#
# Applet configuration
#
#
$config_string = <<'ENDCONFIG';
<XML>
<options>
<geometry x="5" y="5" width="490" height="490" />
<bounds xmin="-5" xmax="5" ymin="-5" ymax="5" tmin="-10" tmax="10" />
<ticks xstep="0.5" ystep="0.5" xsize="5" ysize="5" />
<grid xstep="0.5" ystep="0.5" />
<field xstep="0.5" ystep="0.5" xmin="-4.5" xmax="4.5" ymin="-4.5" ymax="4.5"
color="0x8FBCDB" backgroundcolor="0x153450" />
<solutionstyle thickness="4" color="0xFFCC00" alpha="0.8" />
</options>
<system>
<variable name="t" />
<variable name="y" derivative="v" />
<variable name="v" derivative="-(k/m)*y-(b/m)*v" />
<parameter name="m" value="-3" />
<parameter name="b" value="2" />
<parameter name="k" value="5" />
</system>
</XML>
ENDCONFIG
$applet->configuration($config_string);
|
This is the Applet link section of the problem.
Those portions of the code that begin the line with Notice that the answerBoxAlias line in the configuration has been commented out. This particular applet does not send to WeBWorK any student answer. The applet configuration is all contained between the XML and /XML tags. The top part contains display options for the applet. The following options are configurable:
Next comes the definition of the system of differential equations itself: Each variable is defined in a variable element. The independent variable in this problem is "t", and the dependent variables are "y" and "v". The dependent variables are identified by the derivative attribute, which gives the formula for its derivative with respect to time. Notice that the formulas for the derivatives can include the variables and parameters. Each parameter is defined in a parameter element, and must be initialized properly. For pedagogical reasons, the initial parameters given here don't make sense in terms of the problem, so the student has to think on what are the correct values. |
BEGIN_TEXT
##############################################################
#
# Text
#
#
Context()->texStrings;
BEGIN_TEXT
In this assignment you will use the computer-generated
solutions to analyze three related second-order
differential equations.
$BR
$BR
The most classic of all second-order equations is the
harmonic oscillator:
\[m\frac{d^2y}{dt^2}+b\frac{dy}{dt}+ky=0.\]
(...)
END_TEXT
TEXT( MODES(TeX=>'A graph appears here in the html version.',
HTML=>
$applet->insertAll(
debug=>0,
includeAnswerBox=>0,
# reinitialize_button=>$permissionLevel>=10,
)));
BEGIN_TEXT
$BR
$BR
Are solutions to this system periodic? Explain your answer
in terms of the phase plane plot.
$BR
$BR
\{essay_box()\}
$BR
$BR
If there are periodic solutions, choose a particular initial
condition and estimate the period of the corresponding
solution to two decimal places. Explain how you found this value.
$BR
(...)
Adapted from $BITALIC Differential Equations, 4th Ed., $EITALIC Blanchard, Devaney, Hall, 2012.
END_TEXT
Context()->normalStrings;
|
This is the text section of the problem. The Since the text for this problem is quite large, some parts are omitted. The full problem code can be found at: Differential Equations Essay Style Problem Source. The fragment show, however, shows how to include the applet with the TEXT macro and how to include the essay-style boxes. |
############################################################## # # Answers # # ANS(essay_cmp()); ANS(essay_cmp()); ANS(essay_cmp()); ANS(essay_cmp()); ENDDOCUMENT(); |
This is the answer section of the problem. All answers to this problem are essay-style, and are graded by the instructor. The student receives a note stating that when the problem is submitted.
The |