Difference between revisions of "PolarGraph1"
Paultpearson (talk | contribs) (PGML example link) |
(add historical tag and give links to newer problems.) |
||
| Line 1: | Line 1: | ||
| + | {{historical}} |
||
| + | |||
| + | <p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/Parametric/PolarGraph.html a newer version of this problem]</p> |
||
| + | |||
<h2>Graphing a Parametric or Polar Curve</h2> |
<h2>Graphing a Parametric or Polar Curve</h2> |
||
Latest revision as of 06:19, 18 July 2023
This problem has been replaced with a newer version of this problem
Graphing a Parametric or Polar Curve
This PG code shows how to graph a parametric curve or polar curve with a shading (a filled region).
- File location in OPL: FortLewis/Authoring/Templates/Parametric/PolarGraph1.pg
- PGML location in OPL: FortLewis/Authoring/Templates/Parametric/PolarGraph1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "PGgraphmacros.pl", "AnswerFormatHelp.pl", "unionTables.pl", ); TEXT(beginproblem()); $refreshCachedImages = 1; |
Initialization:
We use |
Context("Numeric")->variables->are(t=>"Real");
$gr = init_graph(-1.1,-1.1,1.1,1.1,axes=>[0,0],size=>[300,300]);
#
# Define some useful colors
#
$gr->new_color("lightblue", 198,217,253); # RGB
$gr->new_color("darkblue", 77,137,249);
$gr->new_color("lightred", 255,127,127);
$gr->new_color("darkred", 255, 55, 55);
$gr->new_color("lightorange", 255,204,127);
$gr->new_color("darkorange", 255, 153, 0);
$gr->new_color("lightgreen", 187, 255, 153);
$gr->new_color("darkgreen", 0, 208, 0);
#
# For a polar curve r = f(t),
# x = r cos(t) = f(t) cos(t)
# y = r sin(t) = f(t) sin(t)
#
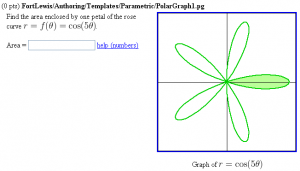
$x = Formula("cos(5*t) * cos(t)");
$y = Formula("cos(5*t) * sin(t)");
$f = new Fun( $x->perlFunction, $y->perlFunction, $gr );
$f->domain(0,3.14);
$f->steps(90);
$f->weight(2);
$f->color('darkgreen');
$gr->fillRegion([0.5,0.1,'lightgreen']);
|
Setup:
We initialize a graph object named |
Context()->texStrings;
BEGIN_TEXT
\{
ColumnTable(
"Find the area enclosed by one petal of the
rose curve \( r = f(\theta) = \cos(5\theta) \).
$BR
$BR
Area = ".
ans_rule(20).$SPACE.
AnswerFormatHelp("numbers")
,
$BCENTER.
image( insertGraph($gr), width=>300, height=>300 ).
$PAR.
"Graph of \( r = \cos(5\theta) \)".
$ECENTER
,
indent => 0, separation => 30, valign => "TOP"
);
\}
END_TEXT
Context()->normalStrings;
|
Main Text:
We use the |
$showPartialCorrectAnswers = 1;
# intentionally incorrect
ANS( Compute("pi")->cmp() );
|
Answer Evaluation: |
Context()->texStrings;
BEGIN_SOLUTION
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |