InverseGraph

Sample Problem with InverseGraph.swf embedded

This sample problem shows how to use this versatile applet.

This applet and WeBWorK problem are based upon work supported by the National Science Foundation under Grant Number DUE-0941388.

A standard WeBWorK PG file with an embedded applet has six sections:

1. A tagging and description section, that describes the problem for future users and authors,
2. An initialization section, that loads required macros for the problem,
3. A problem set-up section that sets variables specific to the problem,
4. An Applet link section that inserts the applet and configures it, (this section is not present in WeBWorK problems without an embedded applet)
5. A text section, that gives the text that is shown to the student, and
6. An answer and solution section, that specifies how the answer(s) to the problem is(are) marked for correctness, and gives a solution that may be shown to the student after the problem set is complete.

The sample file attached to this page shows this; below the file is shown to the left, with a second column on its right that explains the different parts of the problem that are indicated above. A screenshot of the applet embedded in this WeBWorK problem is shown below:

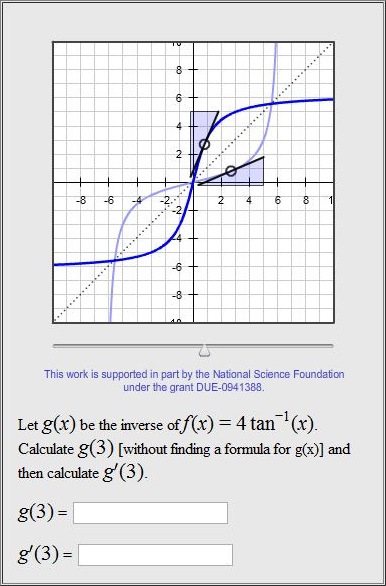
Other useful links:
Flash Applets Tutorial
Things to consider in developing WeBWorK problems with embedded Flash applets

PG problem file	Explanation
##DESCRIPTION ## Inverse Graph ## Sample problem to illustrate ## the use of the InverseGraph.swf ## Flash applet ##ENDDESCRIPTION ## KEYWORDS('calculus','derivatives', ## 'inverse functions') ## DBsubject('Calculus') ## DBchapter('Differentiation') ## DBsection('Derivatives of Inverse Functions') ## Date('8/16/2011') ## Author('Alex Yates') ## Institution('Cleveland State University') ## TitleText1('Calculus: Early Transcendentals 2e') ## EditionText1(2) ## AuthorText1('Rogawski') ## Section1('3.8') ## Problem1('9') ########################################### # This work is supported in part by # the National Science Foundation # under the grant DUE-0941388. ###########################################	This is the tagging and description section of the problem. Note that any line that begins with a "#" character is a comment for other authors who read the problem, and is not interpreted by WeBWorK. The description is provided to give a quick summary of the problem so that someone reading it later knows what it does without having to read through all of the problem code. All of the tagging information exists to allow the problem to be easily indexed. Because this is a sample problem there isn't a textbook per se, and we've used some default tagging values. There is an on-line list of current chapter and section names and a similar list of keywords. The list of keywords should be comma separated and quoted (e.g., KEYWORDS('calculus','derivatives')).
DOCUMENT(); loadMacros( "PGstandard.pl", "AppletObjects.pl", "MathObjects.pl" );	This is the initialization section of the problem. The first executed line of the problem must be the DOCUMENT(); command. Note that every command must end with a semicolon. The loadMacros command loads information that works behind the scenes. For our purposes we can usually just load the macros shown here and not worry about things further.
################################### # Setup ################################### @funcArray = ( "1/4*x^3-1", "x+cos(x)", "1/4*x^3-2*x", "4*atan(x)", "x*atan(x)", "1/2*x^(2)", "x-(x/2)^3" ); @dispArray = ( "\frac{1}{4} x^3 - 1", "x+\cos(x)", "\frac{1}{4} x^3 - 2 x", "4 \tan^{-1}(x)", "x \tan^{-1}(x)", "\frac{1}{2}x^2", "x-(\frac{1}{2}x)^3" ); $rand = random(0,6,1); $func = @funcArray[$rand]; $f = Formula($func); $yval = random(1,3,1); $ans1 = $f->substitute(x=>$yval); $fder = $f->D(); $ans2 = 1/($fder->substitute(x=>$yval));	The GraphLimits.swf applet will accept four different question types, specified with the $qtype variable. These are: limits, continuity, first_derivative and second_derivative. This sample problem is set to 'limits'. The applet has solution/hint information embedded in it. When $hintState=0, this information is not shown. When $hintState=1, this information is revealed. The time parameter tracks the current date and time. The conditional compares that to the due date for the problem set (in the $dueDate scalar variable) and sets $hintState to 1 if the due date has passed and leaves $hintState set to 0 if the assignment is not yet due. The four variables $x1, $x2, $x3 and $x4 are the x-coordinates of four points on the graph that the applet will set to be a removable discontinuity, a jump discontinuity or a cusp. The order of these phenomena is random as are the y-values chosen. The x-coordinates must be between -10 and 10.
################################### # Create link to applet ################################### $appletName = "InverseGraph"; $applet = FlashApplet( codebase => findAppletCodebase("$appletName.swf"), appletName => $appletName, setStateAlias => 'setXML', getStateAlias => 'getXML', setConfigAlias => 'setConfig', height => '400', width => '350', bgcolor => '#e8e8e8', debugMode => 0, submitActionScript => '', );	This is the Applet link section of the problem. If you are embedding a different applet, from the InverseGraph applet, put your applet name in place of 'InverseGraph' in the line $appletName = "InverseGraph";. Enter the height of the applet in the line height => '400', in place of 400 and the width in the line width => '350', in place of 350.
################################### # Configure applet ################################### $applet->configuration(qq{ <XML><Vars func = '$func'/></XML>}); $applet->initialState(qq{ <XML><Vars func = '$func'/></XML>});	The lines $applet->configuration(qq{<XML><Vars func = '$func'/></XML>}); and $applet->initialState(qq{<XML><Vars func = '$func'/></XML>}); configure the applet. The configuration of the applet is done in xml. The variable $func is passed to the applet and set as the function to be graphed.
Context()->texStrings; TEXT(beginproblem()); BEGIN_TEXT $PAR \{ $applet->insertAll(debug=>0, includeAnswerBox=>0, reinitialize_button=>0,) \} $PAR Let \(g(x)\) be the inverse of \(f(x)=$dispArray[$rand]\). Calculate \(g($yval)\) [without finding a formula for g(x)] and then calculate \(g'($yval)\). $PAR \(g($yval)\) = \{ans_rule()\} $PAR \(g'($yval)\) = \{ans_rule()\} END_TEXT	This is the text section of the problem. The TEXT(beginproblem()); line displays a header for the problem, and the Context()->texStrings line sets how formulas are displayed in the text, and we reset this after the text section. Everything between the BEGIN_TEXT and END_TEXT lines (each of which must appear alone on a line) is shown to the student. Mathematical equations are delimited by \( \) (for inline equations) or \[ \] (for displayed equations); in these contexts inserted text is assumed to be TeX code. There are a number of variables that set formatting: $PAR is a paragraph break (like \par in TeX). This page gives a list of variables like this. Finally, \{ \} sets off code that will be executed in the problem text. Here, ans_rule(35) is a function that inserts an answer blank 35 characters wide.
################################### # Answers ################################### ANS(num_cmp($ans1)); ANS(num_cmp($ans2)); ENDDOCUMENT();	This is the answer section of the problem. The problem answer is set by the ANS(num_cmp($ans1));, and ANS(num_cmp($ans2)); lines. These compare the student's answer with the correct answers determined in the problem set-up section. The ENDDOCUMENT(); command is the last command in the file.

License

The Flash applets developed under DUE-0941388 are protected under the following license: Creative Commons Attribution-NonCommercial 3.0 Unported License.