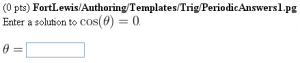Difference between revisions of "PeriodicAnswers1"
Jump to navigation
Jump to search
Paultpearson (talk | contribs) |
(add historical tag and give links to newer problems.) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{historical}} |
||
| + | |||
| + | <p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/Trig/PeriodicAnswers.html a newer version of this problem]</p> |
||
| + | |||
| + | |||
<h2>Periodic Answers</h2> |
<h2>Periodic Answers</h2> |
||
| Line 6: | Line 11: | ||
</p> |
</p> |
||
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Trig/PeriodicAnswers1.pg FortLewis/Authoring/Templates/Trig/PeriodicAnswers1.pg] |
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Trig/PeriodicAnswers1.pg FortLewis/Authoring/Templates/Trig/PeriodicAnswers1.pg] |
||
| − | |||
| + | * PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Trig/PeriodicAnswers1_PGML.pg FortLewis/Authoring/Templates/Trig/PeriodicAnswers1_PGML.pg] |
||
<br clear="all" /> |
<br clear="all" /> |
||
Latest revision as of 05:50, 18 July 2023
This problem has been replaced with a newer version of this problem
Periodic Answers
This PG code shows how to check student answers that are periodic.
- File location in OPL: FortLewis/Authoring/Templates/Trig/PeriodicAnswers1.pg
- PGML location in OPL: FortLewis/Authoring/Templates/Trig/PeriodicAnswers1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", ); TEXT(beginproblem()); |
Initialization: |
Context("Numeric");
$answer = Real("pi/2")->with(period=>pi);
|
Setup: This is self-explanatory. |
Context()->texStrings;
BEGIN_TEXT
Enter a solution to \( \cos(\theta) = 0 \).
$BR
$BR
\( \theta = \)
\{ ans_rule(10) \}
\{ AnswerFormatHelp("angles") \}
END_TEXT
Context()->normalStrings;
|
Main Text: |
$showPartialCorrectAnswers = 1; ANS( $answer->cmp() ); |
Answer Evaluation: |
Context()->texStrings; BEGIN_SOLUTION The cosine of an angle is zero when the angle is an integer multiple of \( \pi \). END_SOLUTION Context()->normalStrings; ENDDOCUMENT(); |
Solution: |