Difference between revisions of "Logarithms1"
Paultpearson (talk | contribs) |
(add historical tag and give links to newer problems.) |
||
| (One intermediate revision by one other user not shown) | |||
| Line 1: | Line 1: | ||
| + | {{historical}} |
||
| + | |||
| + | <p style="font-size: 120%;font-weight:bold">This problem has been replaced with [https://openwebwork.github.io/pg-docs/sample-problems/Algebra/Logarithms.html a newer version of this problem]</p> |
||
| + | |||
| + | |||
<h2>Answer Must Be Simplified Using Logarithms</h2> |
<h2>Answer Must Be Simplified Using Logarithms</h2> |
||
| Line 6: | Line 11: | ||
</p> |
</p> |
||
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Algebra/Logarithms1.pg FortLewis/Authoring/Templates/Algebra/Logarithms1.pg] |
* File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Algebra/Logarithms1.pg FortLewis/Authoring/Templates/Algebra/Logarithms1.pg] |
||
| + | * PGML location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/Algebra/Logarithms1_PGML.pg FortLewis/Authoring/Templates/Algebra/Logarithms1_PGML.pg] |
||
<br clear="all" /> |
<br clear="all" /> |
||
Latest revision as of 05:49, 18 July 2023
This problem has been replaced with a newer version of this problem
Answer Must Be Simplified Using Logarithms
This PG code shows how to disable and undefine some functions and operators, which will require students to simplify their answer using laws of logarithms.
- File location in OPL: FortLewis/Authoring/Templates/Algebra/Logarithms1.pg
- PGML location in OPL: FortLewis/Authoring/Templates/Algebra/Logarithms1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", ); TEXT(beginproblem()); |
Initialization: |
Context("Numeric");
Context()->variables->are(x=>"Real",y=>"Real",z=>"Real");
Context()->variables->set(x=>{limits=>[2,3]});
Context()->variables->set(y=>{limits=>[2,3]});
Context()->variables->set(z=>{limits=>[2,3]});
$a = random(20,40,1);
$b = random(20,40,1);
do { $c = random(20,40,1); } until ( $c != $b );
# TeX
$expr = "\displaystyle \ln \left( \frac{ x^{$a} y^{$b} }{ z^{$c} } \right)";
$answer = Compute("$a * ln(x) + $b * ln(y) - $c * ln(z)");
Context()->operators->undefine("/","^","**");
Context()->functions->undefine("sqrt");
|
Setup:
We add the variables to the context and reset their limits since logarithms are not defined on the default domain |
Context()->texStrings;
BEGIN_TEXT
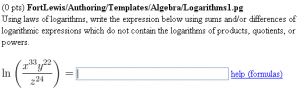
Using laws of logarithms, write the expression
below using sums and/or differences
of logarithmic expressions which do not contain
the logarithms of products, quotients, or powers.
$BR
$BR
\( \displaystyle $expr = \)
\{ ans_rule(40) \}
\{ AnswerFormatHelp("formulas") \}
END_TEXT
Context()->normalStrings;
|
Main Text: |
$showPartialCorrectAnswers = 1; ANS( $answer->cmp() ); |
Answer Evaluation: |
Context()->texStrings;
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |