Difference between revisions of "MatrixAnswer1"
Paultpearson (talk | contribs) (New answer is a matrix template) |
Paultpearson (talk | contribs) (Add more explanatory text) |
||
| Line 1: | Line 1: | ||
| − | <h2>Answer is a Matrix</h2> |
+ | <h2>Answer is a Matrix 1</h2> |
[[File:MatrixAnswer1.png|300px|thumb|right|Click to enlarge]] |
[[File:MatrixAnswer1.png|300px|thumb|right|Click to enlarge]] |
||
| Line 70: | Line 70: | ||
]); |
]); |
||
| − | $B = Matrix([ |
||
| + | $B = Matrix([random(-5,5,1),random(-5,5,1),random(-5,5,1)]); |
||
| − | [random(-5,5,1),random(-5,5,1),random(-5,5,1)], |
||
| − | [random(-5,5,1),random(-5,5,1),random(-5,5,1)], |
||
| − | ]); |
||
$answer = $A * ($B->transpose); |
$answer = $A * ($B->transpose); |
||
| Line 82: | Line 79: | ||
<p> |
<p> |
||
<b>Setup:</b> |
<b>Setup:</b> |
||
| + | The MathObject matrices are constructed using the <code>Matrix()</code> constructor. |
||
| + | The matrix A has two rows and three columns, and is constructed by <code>[ [row 1 entries], [row 2 entries] ]</code>, and this construction generalizes in the obvious way. |
||
| + | If a matrix has only one row, such as B, then it is entered as <code>[row 1 entries]</code> and <b>not</b> as <code>[[row 1 entries]]</code>. |
||
| + | If <code>$B = Matrix([a,b,c]);</code>, then the matrix <code>$B->transpose</code> is equivalent to <code>Matrix([[a],[b],[c]]);</code> which has an outer pair of brackets enclosing all of the rows, where each row encloses its single element with brackets. |
||
</p> |
</p> |
||
</td> |
</td> |
||
Revision as of 20:34, 28 June 2014
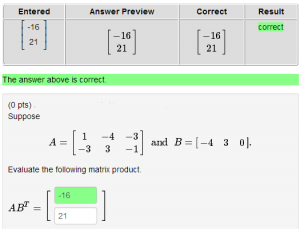
Answer is a Matrix 1
This PG code shows how to evaluate answers that are matrices.
- File location in OPL: FortLewis/Authoring/Templates/LinAlg/MatrixAnswer1.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", ); TEXT(beginproblem()); |
Initialization: |
Context("Matrix");
$A = Matrix([
[random(-5,5,1),random(-5,5,1),random(-5,5,1)],
[random(-5,5,1),random(-5,5,1),random(-5,5,1)],
]);
$B = Matrix([random(-5,5,1),random(-5,5,1),random(-5,5,1)]);
$answer = $A * ($B->transpose);
|
Setup:
The MathObject matrices are constructed using the |
Context()->texStrings;
BEGIN_TEXT
Suppose
\[
A = $A
\ \ \mbox{and} \ \
B = $B.
\]
Evaluate the following matrix product.
$BR
$BR
\( A B^T = \)
\{ $answer->ans_array(5) \}
\{ AnswerFormatHelp("matrices") \}
END_TEXT
Context()->normalStrings;
|
Main Text:
Use the |
$showPartialCorrectAnswers = 1; ANS( $answer->cmp() ); |
Answer Evaluation: Use standard MathObject answer evaluation. |
Context()->texStrings;
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |