Difference between revisions of "UnorderedAnswers1"
Jump to navigation
Jump to search
Paultpearson (talk | contribs) m |
Paultpearson (talk | contribs) m |
||
| Line 167: | Line 167: | ||
[[Category:Top]] |
[[Category:Top]] |
||
| − | [[Category:Authors]] |
||
[[Category:Sample Problems]] |
[[Category:Sample Problems]] |
||
[[Category:Subject Area Templates]] |
[[Category:Subject Area Templates]] |
||
Revision as of 16:28, 3 January 2012
Answers Can Be Entered Into Answer Blanks in Any Order
This PG code shows how to allow students to enter their answers into several answer blanks in any order.
- Download file: File:UnorderedAnswers1.txt (change the file extension from txt to pg when you save it)
- File location in NPL:
FortLewis/Authoring/Templates/Algebra/UnorderedAnswers1.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", "unorderedAnswer.pl", ); TEXT(beginproblem()); |
Initialization:
We must load |
Context("Numeric")->variables->add(y=>"Real",z=>"Real");
$a = random(2,9,1);
$answer1 = Compute("x^$a");
$answer2 = Compute("y^$a");
$answer3 = Compute("z^$a");
|
Setup: |
Context()->texStrings;
BEGIN_TEXT
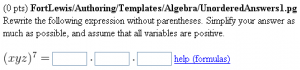
Rewrite the following expression without parentheses.
Simplify your answer as much as possible, and assume
that all variables are positive.
$BR
$BR
\( (xyz)^{$a} = \)
\{ ans_rule(5) \}
\( \cdot \)
\{ ans_rule(5) \}
\( \cdot \)
\{ ans_rule(5) \}
\{ AnswerFormatHelp("formulas") \}
END_TEXT
Context()->normalStrings;
|
Main Text: |
$showPartialCorrectAnswers = 1; UNORDERED_ANS( $answer1->cmp(), $answer2->cmp(), $answer3->cmp(), ); |
Answer Evaluation:
We use $showPartialCorrectAnswers = 0; install_problem_grader(~~&std_problem_grader); |
Context()->texStrings;
BEGIN_SOLUTION
${PAR}SOLUTION:${PAR}
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT('MathObject version.');
ENDDOCUMENT();
|
Solution: |