Logarithms1

Answer Must Be Simplified Using Logarithms

Click to enlarge

This PG code shows how to disable and undefine some functions and operators, which will require students to simplify their answer using laws of logarithms.

• Download file: File:Logarithms1.txt (change the file extension from txt to pg when you save it)
• File location in NPL: FortLewis/Authoring/Templates/Algebra/Logarithms1.pg

Templates by Subject Area

PG problem file	Explanation
Problem tagging data	Problem tagging:
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", "contextLimitedPowers.pl", ); TEXT(beginproblem());	Initialization:
Context("Numeric"); Context()->variables->are(x=>"Real",y=>"Real",z=>"Real"); Context()->variables->set(x=>{limits=>[2,3]}); Context()->variables->set(y=>{limits=>[2,3]}); Context()->variables->set(z=>{limits=>[2,3]}); $a = random(20,40,1); $b = random(20,40,1); do { $c = random(20,40,1); } until ( $c != $b ); # TeX $expr = "\displaystyle \ln \left( \frac{ x^{$a} y^{$b} }{ z^{$c} } \right)"; $answer = Compute("$a * ln(x) + $b * ln(y) - $c * ln(z)"); Context()->operators->undefine("/","^","**"); Context()->functions->undefine("sqrt");	Setup: We add the variables to the context and reset their limits since logarithms are not defined on the default domain [-1,1]. After defining $answer, then we undefine certain operators and functions so that students will have to simplify their answer. Since the answer requires multiplication no matter how it is written, we cannot prevent students from entering an answer such as ln(x*x*x...) instead of $a * ln(x), but by choosing large values for $a, $b, $c, we can strongly discourage them from entering ln(x*x*x...).
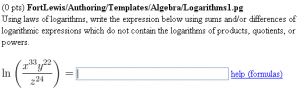
Context()->texStrings; BEGIN_TEXT Using laws of logarithms, write the expression below using sums and/or differences of logarithmic expressions which do not contain the logarithms of products, quotients, or powers. $BR $BR \( \displaystyle $expr = \) \{ ans_rule(40) \} \{ AnswerFormatHelp("formulas") \} END_TEXT Context()->normalStrings;	Main Text:
$showPartialCorrectAnswers = 1; ANS( $answer->cmp() );	Answer Evaluation:
Context()->texStrings; BEGIN_SOLUTION ${PAR}SOLUTION:${PAR} Solution explanation goes here. END_SOLUTION Context()->normalStrings; COMMENT('MathObject version.'); ENDDOCUMENT();	Solution:

Templates by Subject Area