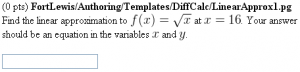Difference between revisions of "LinearApprox1"
Jump to navigation
Jump to search
Paultpearson (talk | contribs) m |
Paultpearson (talk | contribs) |
||
| Line 5: | Line 5: | ||
This PG code shows how to ask a linear approximation question in which the answer is an equation and students receive customized answer hints. |
This PG code shows how to ask a linear approximation question in which the answer is an equation and students receive customized answer hints. |
||
</p> |
</p> |
||
| − | * Download file: [[File:LinearApprox1.txt]] (change the file extension from txt to pg when you save it) |
||
| + | * File location in OPL: [https://github.com/openwebwork/webwork-open-problem-library/blob/master/OpenProblemLibrary/FortLewis/Authoring/Templates/DiffCalc/LinearApprox1.pg FortLewis/Authoring/Templates/DiffCalc/LinearApprox1.pg] |
||
| − | * File location in NPL: <code>FortLewis/Authoring/Templates/DiffCalc/LinearApprox1.pg</code> |
||
<br clear="all" /> |
<br clear="all" /> |
||
| Line 141: | Line 140: | ||
Context()->texStrings; |
Context()->texStrings; |
||
BEGIN_SOLUTION |
BEGIN_SOLUTION |
||
| − | ${PAR}SOLUTION:${PAR} |
||
Solution explanation goes here. |
Solution explanation goes here. |
||
END_SOLUTION |
END_SOLUTION |
||
Revision as of 16:50, 16 June 2013
Linear Approximation With Answer Hints
This PG code shows how to ask a linear approximation question in which the answer is an equation and students receive customized answer hints.
- File location in OPL: FortLewis/Authoring/Templates/DiffCalc/LinearApprox1.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT(); loadMacros( "PGstandard.pl", "MathObjects.pl", "AnswerFormatHelp.pl", "answerHints.pl", "parserAssignment.pl", ); TEXT(beginproblem()); |
Initialization:
We load |
Context("Numeric")->variables->add(y=>"Real");
parser::Assignment->Allow;
$a = random(2,5,1);
$aa = $a**2;
$a2 = 2 * $a;
$f = Compute("sqrt(x)");
$answer = Compute("y = $a + (1/$a2) * (x-$aa)");
|
Setup: We have to tell the context that we are allowing the assignment of a variable to a formula. |
Context()->texStrings;
BEGIN_TEXT
Find the linear approximation to \( f(x) = $f \)
at \( x = $aa \). Your answer should be an
equation in the variables \( x \) and \( y \).
$BR
$BR
\{ ans_rule(20) \}
\{ AnswerFormatHelp("equations") \}
END_TEXT
Context()->normalStrings;
|
Main Text: |
$showPartialCorrectAnswers = 1;
ANS( $answer->cmp()
->withPostFilter(AnswerHints(
[Formula("1/$a2"),Formula("y=1/$a2")] =>
["Your answer should be an equation for a non-horizontal line.",
replaceMessage=>1],
))
);
|
Answer Evaluation: We use answer hints to remind students to enter an equation for a line, not just the slope of the line. |
Context()->texStrings;
BEGIN_SOLUTION
Solution explanation goes here.
END_SOLUTION
Context()->normalStrings;
COMMENT("MathObject version.");
ENDDOCUMENT();
|
Solution: |