Derivative Graph Matching Flash Applet Sample Problem

Sample Problem with derGraphMatchWW.swf embedded

This sample problem shows how to use the derivative graph matching applet.

A standard WeBWorK PG file with an embedded applet has six sections:

1. A tagging and description section, that describes the problem for future users and authors,
2. An initialization section, that loads required macros for the problem,
3. A problem set-up section that sets variables specific to the problem,
4. An Applet link section that inserts the applet and configures it, (this section is not present in WeBWorK problems without an embedded applet)
5. A text section, that gives the text that is shown to the student, and
6. An answer and solution section, that specifies how the answer(s) to the problem is(are) marked for correctness, and gives a solution that may be shown to the student after the problem set is complete.

The sample file attached to this page shows this; below the file is shown to the left, with a second column on its right that explains the different parts of the problem that are indicated above. A screenshot of the applet embedded in this WeBWorK problem is shown below:

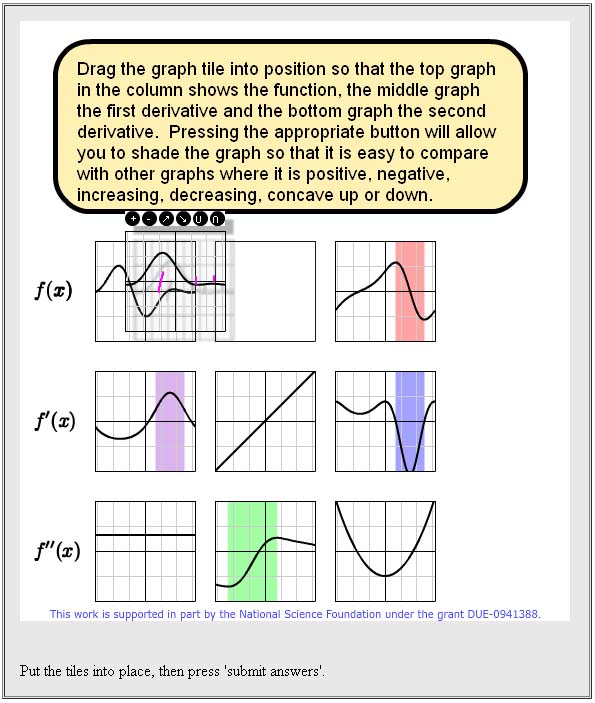
There are other sample problems using applets: GraphLimit Flash Applet Sample Problem, GraphLimit Flash Applet Sample Problem 2

PG problem file	Explanation
##DESCRIPTION ## understanding derivatives graphically ##ENDDESCRIPTION ##KEYWORDS('derivatives', 'graph') ## DBsubject('Calculus') ## DBchapter('Limits and Derivatives') ## DBsection('Derivatives') ## Date('7/25/2011') ## Author('Barbara Margolius') ## Institution('Cleveland State University') ## TitleText1('') ## EditionText1('2011') ## AuthorText1('') ## Section1('') ## Problem1('') ######################################################################## # This work is supported in part by the National Science Foundation # under the grant DUE-0941388. ########################################################################	This is the tagging and description section of the problem. Note that any line that begins with a "#" character is a comment for other authors who read the problem, and is not interpreted by WeBWorK. The description is provided to give a quick summary of the problem so that someone reading it later knows what it does without having to read through all of the problem code. All of the tagging information exists to allow the problem to be easily indexed. Because this is a sample problem there isn't a textbook per se, and we've used some default tagging values. There is an on-line list of current chapter and section names and a similar list of keywords. The list of keywords should be comma separated and quoted (e.g., KEYWORDS('calculus','derivatives')).
DOCUMENT(); # This should be the first executable line in the problem. loadMacros( "PGanswermacros.pl", "PGstandard.pl", "AppletObjects.pl", "MathObjects.pl", );	This is the initialization section of the problem. The first executed line of the problem must be the DOCUMENT(); command. Note that every command must end with a semicolon. The loadMacros command loads information that works behind the scenes. For our purposes we can usually just load the macros shown here and not worry about things further.
# Set up problem TEXT(beginproblem()); $showPartialCorrectAnswers = 1; Context("Numeric"); $ans =Compute("1"); $showSolution = 0; if(time>$dueDate){ $showSolution = 1; } $isit2der = 1; #match first and second derivatives	This is the problem set-up section of the problem. The derGraphMatchWW.swf applet requires the student to match three sets of graphs. If $isit2der is set to zero, the student must match three pairs of graphs of functions and their derivatives. If $isit2der is set to one, the student must match three triples of graphs of functions and their first and second derivatives. The screenshot above shows the applet with $isit2der=1. $showSolutions is turned on when the due date is passed. The solutions are shown within the applet. The problem author can add some explanatory text in the pg file. The applet shows the graphs in the correct positions with shading turned on so that the student can see the function is concave up where its derivative is increasing and the second derivative is positive.
########################################################################## # How to use the Graph_Test applet. # Purpose: The purpose of this applet is to ask graphical limit questions # Use of applet: The applet state consists of the following fields: # qType - question type: limits, continuity, first_derivative, # second_derivative # hintState - context sensitive help is either on or off. # Generally turned on after dueDate # problemSeed - the seed sets the random parameters that control which # graph is chosen. If the seed is changed, the graph is changed. ########################################################################## # qType = first_derivative # get_interval_info - given a type of interval returns a list of intervals # with that characteristic # Valid types are - increasing, decreasing, constant, up, down, straight # up, down and straight pertain to the concavity of the function on the # interval # sample function call: get_interval_info("increasing") # describe_interval - given an interval and a type, the function returns # information about the interval. # Valid types are - # updown (for concavity information), # posneg1 (for sign of first derivative), # posneg2 (for sign of second derviative), # incdec (for whether function is increasing or decreasing on the # interval. # sample function call: describe_interval($x1,$x2,"updown") # right_limits - returns a list of points (a,b) such that # lim_{x\to a^-}f(x)=b, but lim_{x\to a^+}f(x)\= b # left_limits - returns a list of points (a,b) such that # lim_{x\to a^+}f(x)=b, but lim_{x\to a^-}f(x)\= b # neither_limits - returns a list of points (a,b) such that # lim_{x\to a^-}f(x)\=lim_{x\to a^+}f(x)\= f(a)=b # get_intervals returns a list of intervals on which f(x) is continuous. # get_f_of_x - given x value, returns f(x). # returns NaN for x notin [-10,10]. # getf_list - given x value and string returns # "function" - returns f(x) # "leftlimit" - returns lim_{x->a^-}f(x) # "rightlimit" - returns lim_{x->a^+}f(x) # "limit" - returns lim_{x->a}f(x) or "DNE" # # What does the applet do? # The applet draws a graph with jumps, a cusp and discontinuities # When turned on, there is context sensitive help. ############################################################################## ################################### # Create link to applet ################################### $appletName = "Graph_Limit"; $applet = FlashApplet( codebase => findAppletCodebase("$appletName.swf"), appletName => $appletName, appletId => $appletName, setStateAlias => 'setXML', getStateAlias => 'getXML', setConfigAlias => 'setConfig', maxInitializationAttempts => 10, # number of attempts to initialize applet #answerBoxAlias => 'answerBox', height => '475', width => '425', bgcolor => '#ffffff', debugMode => 0, submitActionScript => qq{ getQE("inc").value=getApplet("$appletName").get_interval_info("increasing"); getQE("dec").value=getApplet("$appletName").get_interval_info("decreasing"); getQE("constant").value=getApplet("$appletName").get_interval_info("constant"); }, ); ################################### # Configure applet ################################### # configuration consists of hintState, question type, and random seed, # and x-coordinates of four points where jumps, discontinuities or cusps # occur. $applet->configuration(qq{<xml><hintState>$showHint</hintState><qtype>limits</qtype> <seed>$problemSeed</seed><xlist x1='$x1' x2='$x2' x3='$x3' x4='$x4' /></xml>}); $applet->initialState(qq{<xml><hintState>$showHint</hintState><qtype>limits</qtype> <seed>$problemSeed</seed><xlist x1='$x1' x2='$x2' x3='$x3' x4='$x4' /></xml>}); TEXT( MODES(TeX=>'object code', HTML=>$applet->insertAll( debug=>0, includeAnswerBox=>0, # reinitialize_button=>$permissionLevel>=10, ))); BEGIN_TEXT <input type="hidden" name="inc" id="inc" /> <input type="hidden" name="dec" id="dec" /> <input type="hidden" name="constant" id="constant" /> END_TEXT $answerString1 = $inputs_ref->{inc}; my $correctAnswer1 = List($answerString1); $answerString2 = $inputs_ref->{dec}; my $correctAnswer2 = List($answerString2); $answerString3 = $inputs_ref->{constant}; my $correctAnswer3 = List($answerString3);	This is the Applet link section of the problem. Those portions of the code that begin the line with # are comments and can be omitted or replaced with comments appropriate to your particular problem. You must include the section that follows # Create link to applet. If you are embedding a different applet, from the Graph_Limit applet, put your applet name in place of 'Graph_Limit' in the line $appletName = "Graph_Limit";. Enter the height of the applet in the line height => '475', in place of 475 and the width in the line width => '425', in place of 425. The lines $applet->configuration(qq{<xml><hintState>$hintState</hintState><qtype>$qtype</qtype><seed>$problemSeed</seed><xlist x1='$x1' x2='$x2' x3='$x3' x4='$x4' /></xml>}); and $applet->initialState(qq{<xml><hintState>$hintState</hintState><qtype>$qtype</qtype><seed>$problemSeed</seed><xlist x1='$x1' x2='$x2' x3='$x3' x4='$x4' /></xml>}); configure the applet. The configuration of the applet is done in xml. The hintState is set to the variable $hintState, the question type is set to $qtype and the problem seed is the WeBWorK environmental variable $problemSeed. The variables $x1, $x2, $x3 and $x4 are also passed to the applet. The code qq{ getQE("inc").value=getApplet("$appletName").get_interval_info("increasing"); getQE("dec").value=getApplet("$appletName").get_interval_info("decreasing"); getQE("constant").value=getApplet("$appletName").get_interval_info("constant"); } is called when the 'Submit Answers' button in the problem is pressed. There is an external interface function designed inside the applet. The function name is 'get_interval_info'. These lines of code call the function with javascript. get_interval_info, takes one argument: a string value. The string may be any of the following alternatives: "increasing", "decreasing", "constant", "up", "down" or "straight". get_interval_info returns a list of open intervals with the specified characteristic. The line getQE("inc").value=getApplet("$appletName").get_interval_info("increasing"); gets the value of the function get_interval_info and stores this value in the hidden javascript form field named "inc". Note that although we have carriage returns after each of the 'getQE' statements, you should not have these carriage returns in your pg file. They are here so that the text line will allow display of the code next to the explanation. You will get error messages if you have the carriage returns in your pg file. The hidden form fields are created in the code block: BEGIN_TEXT <input type="hidden" name="inc" id="inc" /> <input type="hidden" name="dec" id="dec" /> <input type="hidden" name="constant" id="constant" /> END_TEXT The applet is configured in the code line: $applet->configuration(qq{<xml><hintState>$hintState</hintState><qtype>limits</qtype> <seed>$problemSeed</seed><xlist x1='$x1' x2='$x2' x3='$x3' x4='$x4' /></xml>}); and the similar line below it. The variables $hintState, $problemSeed, and $x1, $x2, $x3, and $x4 are defined within WeBWorK and used by the applet to set the problem up. TEXT( MODES(TeX=>'object code', HTML=>$applet->insertAll( debug=>0, includeAnswerBox=>0, reinitialize_button=>$permissionLevel>=10, ))); actually embeds the applet in the WeBWorK problem. When the submit button is pressed, the hidden form fields defined in this block are filled with information from the applet. The data from the hidden form fields is used in these simple perl subroutines to define the correct answers to the four questions that are part of this WeBWorK problem. The WeBWorK variable $answerString1 is the content of the hidden form field "inc". $correctAnswer1 is the solution to the first question. The solutions for the next two questions are defined in a similar way.
BEGIN_TEXT $BR $BR list all intervals for which $BR a) \(f^\prime(x)>0\) \{ans_rule(35) \} $BR b) \(f^\prime(x)<0\) \{ans_rule(35) \} $BR c) \(f^\prime(x)=0\) \{ans_rule(35) \} $BR END_TEXT Context()->normalStrings;	This is the text section of the problem. The TEXT(beginproblem()); line displays a header for the problem, and the Context()->texStrings line sets how formulas are displayed in the text, and we reset this after the text section. Everything between the BEGIN_TEXT and END_TEXT lines (each of which must appear alone on a line) is shown to the student. Mathematical equations are delimited by \( \) (for inline equations) or \[ \] (for displayed equations); in these contexts inserted text is assumed to be TeX code. There are a number of variables that set formatting: $PAR is a paragraph break (like \par in TeX). This page gives a list of variables like this. Finally, \{ \} sets off code that will be executed in the problem text. Here, ans_rule(35) is a function that inserts an answer blank 35 characters wide.
############################################################## # # Answers # ## answer evaluators ANS( $correctAnswer1->cmp(strings=>['None']) ); #checks AnSwEr00001 ANS( $correctAnswer2->cmp(strings=>['None']) ); #checks AnSwEr00002 ANS( $correctAnswer3->cmp(strings=>['None']) ); #checks AnSwEr00003 ENDDOCUMENT();	This is the answer section of the problem. The problem answer is set by the ANS( $correctAnswer1->cmp(strings=>['None']) );, ANS( $correctAnswer2->cmp(strings=>['None']) );, ANS( $correctAnswer3->cmp(strings=>['None']) ); lines. These compare the student's answer with the answers returned from the applet. The answers allow for either a list of intervals answer or the string 'None' for empty lists. The solution is embedded in the applet and becomes available when the due date has passed. The ENDDOCUMENT(); command is the last command in the file.