GeneralSolutionODE1
This problem has been replaced with a newer version of this problem
General Solutions to ODEs with Arbitrary Constants
This PG code shows how to write a custom answer checker for ODEs questions where the answer is an equation of the form y = c1 f1(x) + c2 f2(x) + c3 f3(x) for some arbitrary constants c1, c2, c3.
- PGML location in OPL: FortLewis/Authoring/Templates/DiffEq/GeneralSolutionODE1_PGML.pg
| PG problem file | Explanation |
|---|---|
|
Problem tagging: |
|
DOCUMENT();
loadMacros('PGstandard.pl','MathObjects.pl','PGML.pl',
'parserAssignment.pl','PGcourse.pl');
TEXT(beginproblem());
|
Initialization:
We load |
'MathObjects.pl','PGML.pl',
'parserAssignment.pl','PGcourse.pl');
TEXT(beginproblem());
$showPartialCorrectAnswers = 1;
Context('Numeric');
Context()->variables->add(
c1=>'Real',c2=>'Real',c3=>'Real',y=>'Real',
);
Context()->variables->set(
c1=>{limits=>[2,4]},
c2=>{limits=>[2,4]},
c3=>{limits=>[2,4]}
);
Context()->flags->set(
formatStudentAnswer=>'parsed',
reduceConstants=>0,
reduceConstantFunctions=>0,
);
parser::Assignment->Allow;
$a = list_random(2,3,5,6,7,8);
# char poly (r-1)(r^2 + $a)
$answer = Compute("y = c1 e^x + c2 cos(sqrt($a) x) + c3 sin(sqrt($a) x)");
$cmp = $answer->cmp( checker => sub {
my ( $correct, $student, $answerHash ) = @_;
my $stu = Formula($student->{tree}{rop});
#################################
# Check for arbitrary constants
#
Value->Error("Is your answer the most general solution?")
if (
Formula($stu->D('c1'))==Formula(0) ||
Formula($stu->D('c2'))==Formula(0) ||
Formula($stu->D('c3'))==Formula(0)
);
# Linear independence (Wronskian)
my $x = Real(1.43);
my $a11 = $stu->eval('c1'=>1,'c2'=>0,'c3'=>0,x=>$x,y=>0);
my $a12 = $stu->eval('c1'=>0,'c2'=>1,'c3'=>0,x=>$x,y=>0);
my $a13 = $stu->eval('c1'=>0,'c2'=>0,'c3'=>1,x=>$x,y=>0);
my $a21 = $stu->D('x')->eval('c1'=>1,'c2'=>0,'c3'=>0,x=>$x,y=>0);
my $a22 = $stu->D('x')->eval('c1'=>0,'c2'=>1,'c3'=>0,x=>$x,y=>0);
my $a23 = $stu->D('x')->eval('c1'=>0,'c2'=>0,'c3'=>1,x=>$x,y=>0);
my $a31 = $stu->D('x','x')->eval('c1'=>1,'c2'=>0,'c3'=>0,x=>$x,y=>0);
my $a32 = $stu->D('x','x')->eval('c1'=>0,'c2'=>1,'c3'=>0,x=>$x,y=>0);
my $a33 = $stu->D('x','x')->eval('c1'=>0,'c2'=>0,'c3'=>1,x=>$x,y=>0);
Value->Error("Your functions are not linearly independent or your answer is not complete")
if (($a11*($a22*$a33-$a32*$a23)+$a13*($a21*$a32-$a31*$a22)) == ($a12*($a21*$a33-$a31*$a23)));
# Check that the student answer is a solution to the DE
my $stu1 = Formula($stu->D('x'));
my $stu2 = Formula($stu->D('x','x'));
my $stu3 = Formula($stu->D('x','x','x'));
return ($stu3 + $a * $stu1) == ($stu2 + $a * $stu);
});
|
Setup:
Add the arbitrary constants For the
We substitute numerical values that the student is unlikely to choose for Finally, we take several derivatives of the student answer and use them to check that the student answer actually satisfies the differential equation. Again, instead of checking (left side of ODE) == 0, we rearrange the terms of the differential equation to be of the form (some nonzero function) == (some other nonzero function) in order to get a more reliable answer checker.
|
BEGIN_PGML
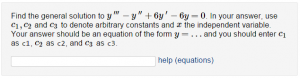
Find the general solution to
[` y^{\,\prime\prime\prime} - y^{\,\prime\prime} + [$a] y^{\,\prime} - [$a] y = 0 `].
In your answer, use [` c_1, c_2 `] and [` c_3 `] to denote arbitrary constants and [` x `]
the independent variable. Your answer should be an equation of the form [`y = \ldots`] and
you should enter [` c_1 `] as [| c1 |]*,
[` c_2 `] as [| c2 |]*, and
[` c_3 `] as [| c3 |]*.
[_________________________________]{$cmp}
[@ helpLink('equations') @]*
END_PGML
|
Main Text: Give students detailed instructions about the format of the answer that is expected. |
BEGIN_PGML_SOLUTION Solution explanation goes here. END_PGML_SOLUTION ENDDOCUMENT(); |
Solution: |