Difference between revisions of "Autonomous solution sketch Flash Applet Sample Problem"
Bmargolius (talk | contribs) |
Bmargolius (talk | contribs) |
||
| Line 285: | Line 285: | ||
|- style=" background-color:#ccffff;" |
|- style=" background-color:#ccffff;" |
||
| <pre> |
| <pre> |
||
| + | ############################################################## |
||
| + | # |
||
| + | # Text |
||
| + | # |
||
| + | # |
||
| + | Context()->texStrings; |
||
| + | BEGIN_TEXT |
||
| + | Even before you learn techniques for solving differential equations, you may be able to analyze equations $BITALIC qualitatively$EITALIC. As an example, look at the nonlinear equation \(\frac{dy}{dt}=$expr.\) You are going to analyze the solutions, \(y\), of this equation without actually finding them. You will be asked to sketch three solutions of the differential equation on the graph below based on qualitative information from the differential equation. |
||
| + | $BR |
||
| + | $BR |
||
| + | In what follows, picture the \(t-\)axis running horizontally and the \(y-\)axis running vertically. |
||
| + | $BR$BR |
||
| + | a) For what values of \(y\) is the graph of \(y\) as a function of \(t\) increasing? Use interval notation for your answer. \{ AnswerFormatHelp("intervals") \} \{ ans_rule(20) \}$BR |
||
| + | $BR |
||
| + | $BR |
||
| + | |||
| + | b) For what values of \(y\) is the graph of \(y\) concave up? \{ ans_rule(20) \} \{AnswerFormatHelp("intervals") \} $BR |
||
| + | For what values of \(y\) is it concave down? \{ ans_rule(20) \} \{AnswerFormatHelp("intervals") \} |
||
| + | $BR |
||
| + | What information do you need to answer a question about concavity? Remember that \(y\) is an implicit function of \(t\). $BR |
||
| + | $BR |
||
| + | $BR |
||
| + | |||
| + | c) Say you are given the initial condition \(y(0)=$blueICy\). Use the information found in parts (a) and (b) to sketch the graph of \(y\) in the applet provided. Draw the curve in $BBOLD\{ BBLUE() \} blue\{ EBLUE() \}$EBOLD. What is the $BITALIC long-term$EITALIC behavior of \(y(t)\)? That is, what is \(\lim_{t\to\infty}y(t)\)? \{ ans_rule(10) \}$BR |
||
| + | $BR |
||
| + | END_TEXT |
||
| + | TEXT( MODES(TeX=>'object code', HTML=>$applet->insertAll( |
||
| + | debug=>0, |
||
| + | includeAnswerBox=>1, |
||
| + | # reinitialize_button=>$permissionLevel>=10, |
||
| + | ))); |
||
| + | |||
| + | BEGIN_TEXT |
||
| + | $BR$BR |
||
| + | |||
| + | d) Say you are given the initial condition |
||
| + | \(y(0)=$pinkICy\). Use the information found |
||
| + | in parts (a) and (b) to sketch the graph of \(y\). |
||
| + | Draw the curve on the applet used in part (c). |
||
| + | Draw the curve in $BBOLD\{ BPINK() \}pink |
||
| + | \{ EPINK() \}$EBOLD(pink). What is the |
||
| + | $BITALIC long-term$EITALIC behavior of |
||
| + | \(y(t)\)? That is, what is |
||
| + | \(\lim_{t\to\infty}y(t)\)? \{ ans_rule(10) \}$BR |
||
| + | $BR |
||
| + | $BR |
||
| + | |||
| + | e) Sketch the graph of \(y\) if \(y(0)=$yellowICy\). |
||
| + | (Look at the original equation.) Sketch this curve in |
||
| + | $BBOLD\{ BYELLOW() \}yellow\{ EYELLOW() \} |
||
| + | $EBOLD(yellow). $BR |
||
| + | $BR |
||
| + | $BR |
||
| + | |||
| + | f) If \(y(t)\) represents the population of |
||
| + | some animal species, and if units on the \(y-\)axis |
||
| + | are in thousands, interpret the results of (c), |
||
| + | (d) and (e). |
||
| + | $BR |
||
| + | The solution to part (c) (sketched in |
||
| + | $BBOLD\{ BBLUE() \} blue\{ EBLUE() \} |
||
| + | $EBOLD) represents: \{ $popup1->menu() \}$BR |
||
| + | $BR |
||
| + | The solution to part (d) (sketched in |
||
| + | $BBOLD\{ BPINK() \}pink\{ EPINK() \} |
||
| + | $EBOLD)(pink) represents: \{ $popup2->menu() \}$BR |
||
| + | $BR |
||
| + | The solution to part (e) (sketched in |
||
| + | $BBOLD\{ BYELLOW() \}yellow\{ EYELLOW() \} |
||
| + | $EBOLD(yellow)) represents: \{ $popup3->menu() \}$BR |
||
| + | $BR |
||
| + | |||
| + | Adapted from $BITALIC A Modern Introduction to |
||
| + | Differential Equations, 2nd Ed., $EITALIC |
||
| + | Henry J. Ricardo, 2009. |
||
| + | |||
| + | END_TEXT |
||
</pre> |
</pre> |
||
| <p> |
| <p> |
||
Revision as of 10:24, 10 August 2013
Flash Applets embedded in WeBWorK questions Autonomous solution sketch Example
Sample Problem with sketch_3.swf embedded
This sample problem shows how to use this versatile applet.
This applet and WeBWorK problem are based upon work supported by the National Science Foundation under Grant Number DUE-0941388.
Click here to see a problem like this in action: [1]
A standard WeBWorK PG file with an embedded applet has six sections:
- A tagging and description section, that describes the problem for future users and authors,
- An initialization section, that loads required macros for the problem,
- A problem set-up section that sets variables specific to the problem,
- An Applet link section that inserts the applet and configures it, (this section is not present in WeBWorK problems without an embedded applet)
- A text section, that gives the text that is shown to the student, and
- An answer and solution section, that specifies how the answer(s) to the problem is(are) marked for correctness, and gives a solution that may be shown to the student after the problem set is complete.
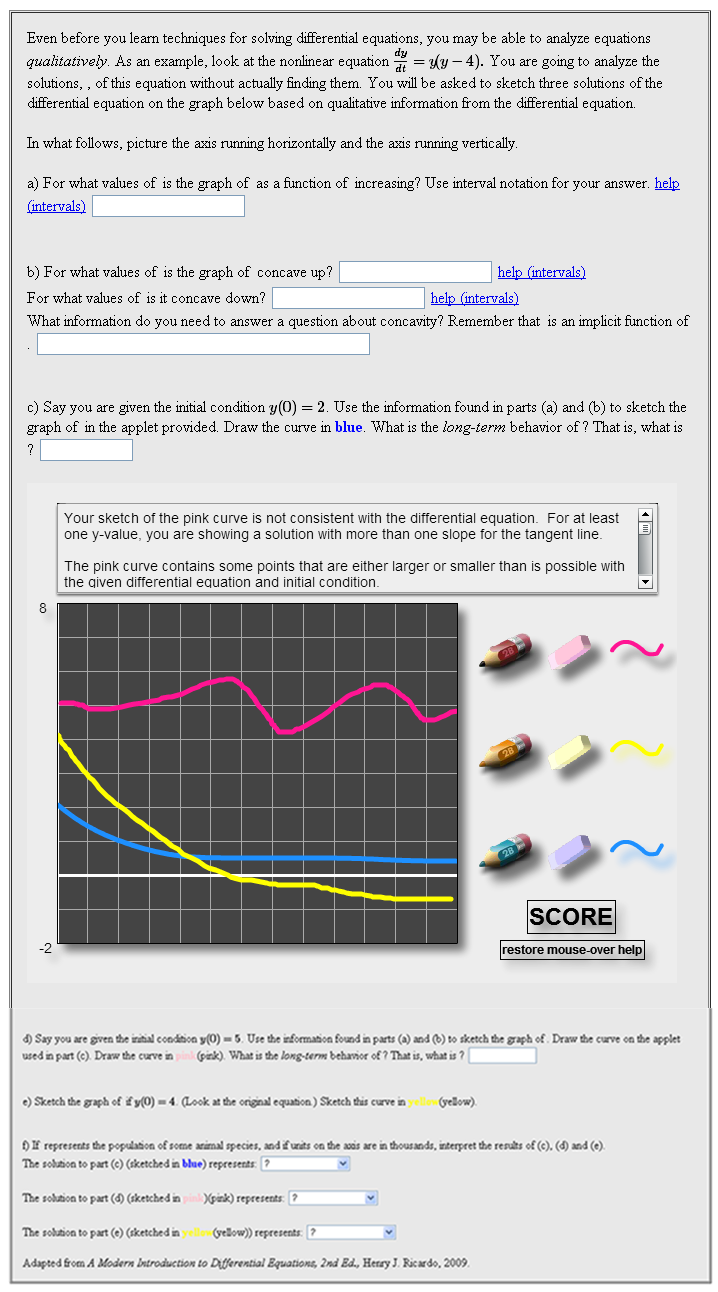
The sample file attached to this page shows this; below the file is shown to the left, with a second column on its right that explains the different parts of the problem that are indicated above. A screenshot of the applet embedded in this WeBWorK problem is shown below:
There are other problems using applets:
Derivative Graph Matching Flash Applet Sample Problem
GraphSketch Flash Applet Sample Problem 1
USub Applet Sample Problem
trigwidget Applet Sample Problem
solidsWW Flash Applet Sample Problem 1
solidsWW Flash Applet Sample Problem 2
solidsWW Flash Applet Sample Problem 3
Hint Applet (Trigonometric Substitution) Sample Problem
phasePortrait Flash Applet Sample Problem 1
Other useful links:
Flash Applets Tutorial
Things to consider in developing WeBWorK problems with embedded Flash applets
| PG problem file | Explanation |
|---|---|
##DESCRIPTION
## Sketch autonomous solutions to polynomial differential equation
##ENDDESCRIPTION
##KEYWORDS('logistic', 'population')
## DBsubject('Differential Equations')
## DBchapter('Introduction')
## DBsection('Autonomous Differential Equations')
## Date('8/9/2013')
## Author('L. Felipe Martins')
## Author('Barbara Margolius')
## Institution('Cleveland State University')
## TitleText1('Differential Equations')
## EditionText1('2')
## AuthorText1('Ricardo')
## Chapter('1')
## Problem1('1_1')
###########################################
# This work is supported in part by
# the National Science Foundation
# under the grant DUE-0941388.
###########################################
|
This is the tagging and description section of the problem. Note that any line that begins with a "#" character is a comment for other authors who read the problem, and is not interpreted by WeBWorK. The description is provided to give a quick summary of the problem so that someone reading it later knows what it does without having to read through all of the problem code. All of the tagging information exists to allow the problem to be easily indexed. Because this is a sample problem there isn't a textbook per se, and we've used some default tagging values. There is an on-line list of current chapter and section names and a similar list of keywords. The list of keywords should be comma separated and quoted (e.g., KEYWORDS('calculus','derivatives')). |
DOCUMENT();
loadMacros(
"PGstandard.pl", # Standard macros for PG language
"MathObjects.pl",
"parserPopUp.pl",
"AppletObjects.pl",
"AnswerFormatHelp.pl",
"PGasu.pl",
);
sub BPINK {
MODES(TeX => '{\\color{pink} ', HTML => '<span style="color:pink">');
};
sub EPINK {
MODES( TeX => '}', HTML => '</span>');
};
sub BBLUE {
MODES(TeX => '{\\color{blue} ', HTML => '<span style="color:blue">');
};
sub EBLUE {
MODES( TeX => '}', HTML => '</span>');
};
sub BYELLOW {
MODES(TeX => '{\\color{yellow} ', HTML => '<span style="color:yellow">');
};
sub EYELLOW {
MODES( TeX => '}', HTML => '</span>');
};
# Print problem number and point value (weight) for the problem
TEXT(beginproblem());
# Show which answers are correct and which ones are incorrect
$showPartialCorrectAnswers = 1;
|
This is the initialization section of the problem. The first executed line of the problem must be the
The |
##############################################################
#
# Setup
#
#
Context("Numeric");
Context()->variables->add(y=>"Real");
$a = -random(1,4,1);
$expr = Formula("y*(y+$a)")->reduce();
$ymax = Compute("-$a+4");
$I1=Compute("(-infinity,0)");
$I2=Compute("(0,-$a)");
$I3=Compute("(-$a,infinity)");
$cup = Compute("(0,-$a/2)U(-$a,infinity)");
$cdown = Compute("(-infinity,0)U(-$a/2,-$a)");
$lim1 = Compute("0");
$popup1 = PopUp(["?", "extinction", "equilibrium",
"explosive growth"], "extinction");
$popup2 = PopUp(["?", "extinction", "equilibrium",
"explosive growth"], "explosive growth");
$popup3 = PopUp(["?", "extinction", "equilibrium",
"explosive growth"], "equilibrium");
$inc = Compute("$I1 U $I3");
$lim2 = Compute("infinity");
$boardMessage = "Sketch three solutions to this
differential equation using the information
given in the problem.";
# applet adds a point for each error it detects.
# It records 100 if the graphs are not drawn
$ans = Compute("0");
#+++++++++++++++++++++++++++++++++++++++++++++
# Designate characteristics of pink curve
# min is IC, max is ymax; concave up on ($IC,ymax);
# increasing on ($IC,ymax)
# note intervals are in y not t
$pinkICy = Compute("-$a+1");
$pinkIntervalsIncLow = $pinkICy;
$pinkIntervalsIncHigh = $ymax;
$pinkIntervalsCupLow = $pinkICy;
$pinkIntervalsCupHigh = $ymax;
$pinkMin = $pinkICy;
#+++++++++++++++++++++++++++++++++++++++++++++
# Designate characteristics of blue curve
# min is IC, max is ymax; concave down on (0,$IC);
# decreasing on (0,$IC)
# note intervals are in y not t
$blueICy = Compute("-$a/2");
$blueIntervalsDecLow = 0;
$blueIntervalsIncHigh = $blueICy;
$blueIntervalsCupLow = 0;
$blueIntervalsCupHigh = $blueICy;
$blueMax = $blueICy;
$blueMin = 0;
#+++++++++++++++++++++++++++++++++++++++++++++
# Designate characteristics of blue curve
# min is IC, max is IC; horizontal line
# note intervals are in y not t
$yellowICy = Compute("-$a");
$yellowMax = $yellowICy;
$yellowMin = $yellowICy;
|
The sketch_3.swf applet requires the student to sketch three solution curves. The problem author specifies initial conditions, intervals of increase, intervals of decrease, intervals of concavity, and the maximum and minimum possible values of the curves. |
###################################
# Create link to applet
###################################
$appletName = "sketch_3";
$applet = FlashApplet(
codebase => findAppletCodebase("$appletName.swf"),
appletName => $appletName,
appletId => $appletName,
setStateAlias => 'setXML',
getStateAlias => 'getXML',
setConfigAlias => 'setConfig',
getConfigAlias => 'getConfig',
maxInitializationAttempts => 5, # number of attempts to initialize applet
answerBoxAlias => 'answerBox',
height => '500',
width => '650',
bgcolor => '#ededed',
debugMode => 0,
submitActionScript =>
qq{getQE("answerBox").value=getApplet("$appletName").getAnswer() },
);
|
This is the Applet link section of the problem.
You must include the section that
follows |
$config_string = <<"ENDCONFIG";
<XML>
<boardMessage>$boardMessage</boardMessage>
<xmin>0</xmin><xmax>13</xmax><ymin>-2</ymin><ymax>$ymax</ymax>
<depVar>y</depVar><indVar>t</indVar>
<showSolution>false</showSolution>
<blueIntervalsCup>
<interval left='0' right='$blueICy'></interval></blueIntervalsCup>
<blueIntervalsDec>
<interval left='0' right='$blueICy'></interval>
</blueIntervalsDec>
<pinkIntervalsInc>
<interval left='$pinkICy' right='$ymax'></interval>
</pinkIntervalsInc>
<pinkIntervalsCup>
<interval left='$pinkICy' right='$ymax'></interval>
</pinkIntervalsCup>
<blueMax>$blueMax</blueMax>
<blueMin>$blueMin</blueMin>
<pinkMin>$pinkMin</pinkMin>
<yellowMin>$yellowMin</yellowMin>
<yellowMax>$yellowMax</yellowMax>
<pinkICy>$pinkICy</pinkICy>
<blueICy>$blueICy</blueICy>
<yellowICy>$yellowICy</yellowICy>
<pinkMaxX>0.2</pinkMaxX>
</XML>
ENDCONFIG
$applet->configuration($config_string);
$applet->initialState($config_string);
|
The XML here conveys to the applet what each curve should look like. The code |
##############################################################
#
# Text
#
#
Context()->texStrings;
BEGIN_TEXT
Even before you learn techniques for solving differential equations, you may be able to analyze equations $BITALIC qualitatively$EITALIC. As an example, look at the nonlinear equation \(\frac{dy}{dt}=$expr.\) You are going to analyze the solutions, \(y\), of this equation without actually finding them. You will be asked to sketch three solutions of the differential equation on the graph below based on qualitative information from the differential equation.
$BR
$BR
In what follows, picture the \(t-\)axis running horizontally and the \(y-\)axis running vertically.
$BR$BR
a) For what values of \(y\) is the graph of \(y\) as a function of \(t\) increasing? Use interval notation for your answer. \{ AnswerFormatHelp("intervals") \} \{ ans_rule(20) \}$BR
$BR
$BR
b) For what values of \(y\) is the graph of \(y\) concave up? \{ ans_rule(20) \} \{AnswerFormatHelp("intervals") \} $BR
For what values of \(y\) is it concave down? \{ ans_rule(20) \} \{AnswerFormatHelp("intervals") \}
$BR
What information do you need to answer a question about concavity? Remember that \(y\) is an implicit function of \(t\). $BR
$BR
$BR
c) Say you are given the initial condition \(y(0)=$blueICy\). Use the information found in parts (a) and (b) to sketch the graph of \(y\) in the applet provided. Draw the curve in $BBOLD\{ BBLUE() \} blue\{ EBLUE() \}$EBOLD. What is the $BITALIC long-term$EITALIC behavior of \(y(t)\)? That is, what is \(\lim_{t\to\infty}y(t)\)? \{ ans_rule(10) \}$BR
$BR
END_TEXT
TEXT( MODES(TeX=>'object code', HTML=>$applet->insertAll(
debug=>0,
includeAnswerBox=>1,
# reinitialize_button=>$permissionLevel>=10,
)));
BEGIN_TEXT
$BR$BR
d) Say you are given the initial condition
\(y(0)=$pinkICy\). Use the information found
in parts (a) and (b) to sketch the graph of \(y\).
Draw the curve on the applet used in part (c).
Draw the curve in $BBOLD\{ BPINK() \}pink
\{ EPINK() \}$EBOLD(pink). What is the
$BITALIC long-term$EITALIC behavior of
\(y(t)\)? That is, what is
\(\lim_{t\to\infty}y(t)\)? \{ ans_rule(10) \}$BR
$BR
$BR
e) Sketch the graph of \(y\) if \(y(0)=$yellowICy\).
(Look at the original equation.) Sketch this curve in
$BBOLD\{ BYELLOW() \}yellow\{ EYELLOW() \}
$EBOLD(yellow). $BR
$BR
$BR
f) If \(y(t)\) represents the population of
some animal species, and if units on the \(y-\)axis
are in thousands, interpret the results of (c),
(d) and (e).
$BR
The solution to part (c) (sketched in
$BBOLD\{ BBLUE() \} blue\{ EBLUE() \}
$EBOLD) represents: \{ $popup1->menu() \}$BR
$BR
The solution to part (d) (sketched in
$BBOLD\{ BPINK() \}pink\{ EPINK() \}
$EBOLD)(pink) represents: \{ $popup2->menu() \}$BR
$BR
The solution to part (e) (sketched in
$BBOLD\{ BYELLOW() \}yellow\{ EYELLOW() \}
$EBOLD(yellow)) represents: \{ $popup3->menu() \}$BR
$BR
Adapted from $BITALIC A Modern Introduction to
Differential Equations, 2nd Ed., $EITALIC
Henry J. Ricardo, 2009.
END_TEXT
|
|
TEXT(MODES(TeX=>"", HTML=><<'END_TEXT'));
<script>
if (navigator.appVersion.indexOf("MSIE") > 0) {
document.write("<div width='3in'
align='center' style='background:yellow'>
You seem to be using Internet Explorer.
<br/>It is recommended that another
browser be used to view this page.</div>");
}
</script>
END_TEXT
|
The text between the |
BEGIN_TEXT
$BR
The graph shown is for the
function \(f(x)\).
$BR Compute the following
quantities:
$BR
a)
\(f($x1)=\)
\{ans_rule(35) \}
$BR
b)
\(\lim_{x\to {$x2}^+}f(x)=\)
\{ans_rule(35) \}
$BR
c)
\(\lim_{x\to {$x3}^-}f(x)=\)
\{ans_rule(35) \}
$BR
d)
\(\lim_{x\to {$x4}}f(x)=\)
\{ans_rule(35) \}
$BR
END_TEXT
Context()->normalStrings;
|
This is the text section
of the problem. The
Mathematical equations are delimited by
There are a number of variables that set
formatting: |
############################# # # Answers # ## answer evaluators ANS( $correctAnswer1->cmp() ); #checks AnSwEr00001 ANS( $correctAnswer2->cmp() ); #checks AnSwEr00002 ANS( $correctAnswer3->cmp() ); #checks AnSwEr00003 ANS(num_cmp($correctAnswer4, strings=>['DNE'])); #checks AnSwEr00004 ENDDOCUMENT(); |
This is the answer
section of the problem. The problem answer
is set by the The solution is embedded in the applet and becomes available when the due date has passed.
The |