WeBWorK Problems

help with Fraction type

help with Fraction type

by Giorgi Shonia -
Number of replies: 4
Appreciate if someone please could help why the following code is failing. Interestingly, if I put Compute instead of Real (bold red line) it works. I'm also attaching screenshot of error message, it shows the "same" submitted=correct answer, but incorrect status. 

##DESCRIPTION
##  Algebra problem: true or false for inequality 
##ENDDESCRIPTION

##KEYWORDS('algebra', 'inequality', 'fraction')

## DBsubject('Algebra')
## DBchapter('Fundamentals')
## DBsection('Real Numbers')
## Date('6/3/2002')
## Author('Giorgi Shonia')
## Institution('')
## TitleText1('Precalculus')
## EditionText1('3')
## AuthorText1('Stewart, Redlin, Watson')
## Section1('1.1')
## Problem1('22')

########################################################################

DOCUMENT();      

loadMacros(
   "PGstandard.pl",     # Standard macros for PG language
   "MathObjects.pl",
   "contextFraction.pl",
   "unionTables.pl"
   #"contextLimitedPowers.pl"
   #"source.pl",        # allows code to be displayed on certain sites.
   #"PGcourse.pl",      # Customization file for the course
);

# Print problem number and point value (weight) for the problem
TEXT(beginproblem());

# Show which answers are correct and which ones are incorrect
$showPartialCorrectAnswers = 1;

# #############################################################
# #
#  Setup
#
#

Context("Numeric");
#Context()->flags->set(
#  tolerance => 0.01,
#  tolType => "absolute",
#);

do {$a=Real(random(6, 8, 0.01))} while ((10*($a-floor($a))==0));

$b=Real(100*(7.62-7));
#$b=62;
Context("Fraction");
$f=Fraction($b,100);

##############################################################
#
#  Text
#
#

Context()->texStrings;
BEGIN_TEXT

Please simplify, convert decimal into fraction and percentage. Please use at least 2 digits precision for percentage. Please enter fraction in two separate boxes as whole and (reduced) fraction part, eg 7 2/5. $BR
\[$a\]
\[$b\]
 \{$f->ans_rule(10)\} $BR $BR

END_TEXT
Context()->normalStrings;

##############################################################
#
#  Answers
#
#


ANS($f->cmp);

# relative tolerance --3.1412 is incorrect but 3.1413 is correct
# default tolerance is .01 or one percent.


ENDDOCUMENT();        
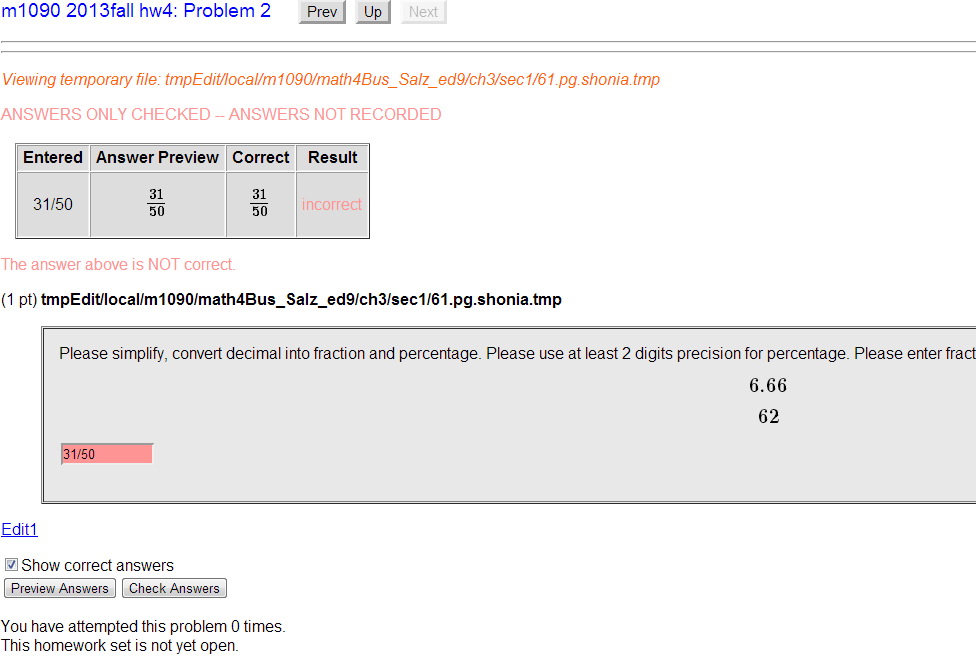
Attachment wwDebug.png
In reply to Giorgi Shonia

Re: help with Fraction type

by Davide Cervone -
It turns out that there is a small issue with the Fraction MathObject class that doesn't usually show up, but does in your case. The issue is that 100*(7.62-7) is not actually equal to 62. In the conversion to binary, some things are repeating "decimals" (binimals?) that are not repeating in base 10 (for example, .1 is a repeating decimal in binary notation), and so they get truncated when stored on a computer. When you multiply by 100, you don't necessarily get back the integer you expect because of the loss of the tail of the decimal.

In your case, it turns out that 62 - 100*(7.62-7) equals about 1.421E-14, a very small number, but non-zero none the less. So when your $b value is used in the fraction, result is not actually equal to 62/100.

The issue with the Fraction object is that it is not comparing the correct and student answers using the "fuzzy" tolerances, but is doing a direct perl real comparison. That is OK when the numerator and denominator are actual integers, but not when they are reals very close to an integer, as in your case.

One way to resolve this is to use 

    $b = Real(round(100*(7.62-7)));
to force it to be an integer prior to putting it into the fraction.

The reason why using Compute() worked is that it first converts its input to a string (and since it is 62 plus a very small number, the string conversion just shows 62 Then it converts this back to a number, and so the result actually is the integer 62, not a real number very close to it. So the fraction works in that case.

I will want to do something to the Fraction class to make this work more easily, but I'm not sure which way to do it. I could use round() on the arguments to Fraction() automatically, so you don't have to, which might make sense to do. Or I could do the comparison of Fractions using the tolerances from the Context. That might be better, except that it would mean that some different fractions might be treated as equal of the tolerances are not tight enough. For example 12345/100000 would equal 12344/100000 with the default tolerances. So I'm not sure which is the better approach.

In reply to Davide Cervone

Re: help with Fraction type

by Alex Jordan -
This may be relevant - maybe not. But it's something I have though about asking Davide about.

contextFraction.pl has this subroutine in it:
 
#
# Convert a real to a reduced fraction approximation
#
sub toFraction {
 my $context = shift; my $x = shift;
 my $Real = $context->Package("Real");
 my $d = 1000000;
 my ($a,$b) = reduce(int($x*$d),$d);
 return [$Real->make($a),$Real->make($b)];
} 
This has the not-so-nice effect of turning the real 1/3 into the Fraction 333333/1000000. Fractions created this way must have denominators built from 2s and 5s.

Instead, if this subroutine used a continued fraction algorithm tweaked in the right way, then not only would 1/3 stay put as 1/3, but also 62 - 1.421E-14 would become 62/1. Numbers like pi would become 355/113 after only four iterations of the algorithm, rather than 3141593/1000000.

I could give a continued fraction algorithm, but there are probably better ones out there in the internet. I think a key ingredient would be that, at the stage where you take the reciprocal, if that number is very small, like smaller than the zeroLevel, then the algorithm should terminate early. (It absolutely has to terminate if the number is 0). This would allow 62 - 1.421E-14 to become 62, and also 0.333333333333333 to become 1/3.

And there would be other considerations: how many iterations are necessary to allow for denominators on the order of 1000000? how many iterations would be too many: so many that rounding error could creep in and actually affect the integers that are stored as part of the continued fraction process? I'm curious what Davide or any other developers think.


 
                                    

                
                
                
                                        
                
                
                                            

                                                    
                                            

                
                                        
                                

                            

                        

                    

                
        

                

                    

                        
                
                        

                            

                                        

                                                
                                        

                                

                                        In reply to Alex Jordan
                                        
Re: help with Fraction type

                                        

                                            by Alex Jordan - 
                                        

                                

                            

                
                            

                                        

                                        

                
                                

                                    

                                        Here is some code I have been using for this. The Fraction context needs to be in use.
contFrac(x,n) 
returns a Fraction that is very close to x using continued fraction approximation. The function is recursive and n is a depth countdown. Using 30 for n will ensure that any rational value for x with six-digit (or less) denominator will be caught and output as a Fraction equal to x. (This also catches many rationals with larger denominators.)

For irrationals and other rationals with bigger denominators, either the algorithm stops after n iterations or when the kth integer part is over 10^8. For example, contFrac(10+10**-9,n) will always output Fraction(10,1). But contFrac(10+10**-8,1) will output Fraction(999999911,99999991).

sub contFrac {
 my $real = shift;
 my $counter = shift;
 my $intpart = floor($real);
 my $partial;
 if (($real - $intpart > 1/10**8) and ($counter>0))
 {$partial = contFrac(1/($real - $intpart ), $counter-1);}
 else {return Fraction($intpart,1)};
 return 1/$partial+$intpart ;
};
 
                                    

                
                
                
                                        
                
                
                                            

                                                    
                                            

                
                                        
                                

                            

                        

                    

                
        

        

                

        

                

                

                    

                        
                
                        

                            

                                        

                                                
                                        

                                

                                        In reply to Davide Cervone
                                        
Re: help with Fraction type

                                        

                                            by Giorgi Shonia - 
                                        

                                

                            

                
                            

                                        

                                        

                
                                

                                    

                                        thx Davide, this is helpful. 

related (full code below). I create Fractons $np and $bp, Reals $nq and $bq and then calculate $t1=Real(($np*$nq)+($bp*$bq)) which I convert back to LimitedProperFraction, which is to be entered an (fraction) answer. I realize this is a poor practice? With bringing Real in the middle of calculation I create some approximations, which when converted back to fraction will create nearby, but different (then calculated using algebra arithmetic) rational? I am attaching a screenshot of such error (seed 10). Should I have kept everything in Fraction and overloaded operations would use fraction arithmetic?

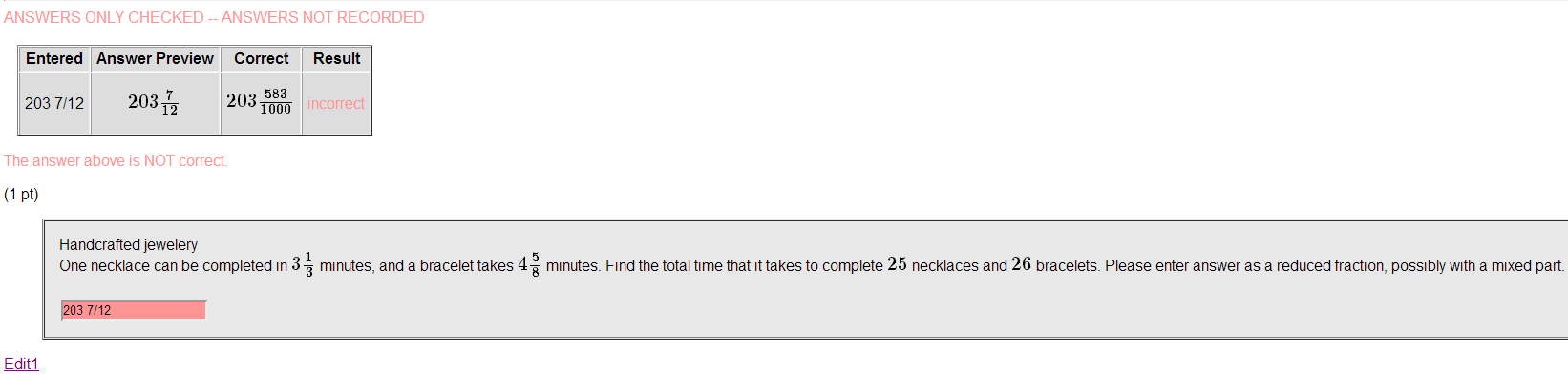
##DESCRIPTION
##  Algebra problem: true or false for inequality 
##ENDDESCRIPTION

##KEYWORDS('algebra', 'inequality', 'fraction')

## DBsubject('Algebra')
## DBchapter('Fundamentals')
## DBsection('Real Numbers')
## Date('6/3/2002')
## Author('')
## Institution('')
## TitleText1('Precalculus')
## EditionText1('3')
## AuthorText1('Stewart, Redlin, Watson')
## Section1('1.1')
## Problem1('22')

########################################################################

DOCUMENT();      

loadMacros(
   "PGstandard.pl",     # Standard macros for PG language
   "MathObjects.pl",
   "contextFraction.pl"
   #"source.pl",        # allows code to be displayed on certain sites.
   #"PGcourse.pl",      # Customization file for the course
);

# Print problem number and point value (weight) for the problem
TEXT(beginproblem());

# Show which answers are correct and which ones are incorrect
#$showPartialCorrectAnswers = 1;

##############################################################
#
#  Setup
#
#
#Context("Numeric");
#Context()->flags->set(
#tolerance=>0.001,
#tolType=>"absolute");

foreach my $i ($np, $bp){
$q=Real(random(3,9,1));
$p=Real(random(2*$q+1,5*$q,1));
while (gcd($p,$q)==$q){$p=Real(random(2*$q+1,5*$q,1));}
Context("LimitedProperFraction");
$i=Fraction($p,$q);
}

# this code it bad. Staring with reals, calculation and then fraction, creates #cumulative precision error

$nq=Real(random(20,40,1));
$bq=Real(random(15,35,1));
$t1=Real(($np*$nq)+($bp*$bq));
Context("LimitedProperFraction");
#Context()->flags->set(showMixedNumbers=>0);
$a=Fraction("$t1");



##############################################################
#
#  Text
#
#

Context()->texStrings;
BEGIN_TEXT

Handcrafted jewelery
$BR
One necklace can be completed in \($np\) minutes, and a bracelet takes \($bp\) minutes. Find the total time that it takes to complete \($nq\) necklaces and \($bq\) bracelets.

Please enter answer as a reduced fraction, possibly with a mixed part. 

$BR $BR
\{$a->ans_rule\}
$BR
END_TEXT
Context()->normalStrings;

##############################################################
#
#  Answers
#
#

ANS($a->cmp);
# relative tolerance --3.1412 is incorrect but 3.1413 is correct
# default tolerance is .01 or one percent.


ENDDOCUMENT();        

                                    

                
                
                                                

                                                    Attachment wwDebug_2.png