The way homework totals are rounded for the student and instructor views within WeBWorK vs. the downloadable score files is different, which can lead to students complaining about score discrepancies. I see that this was reported in 2007, but there wasn't a reply, and apparently the issue is still present:
http://webwork.maa.org/moodle/mod/forum/discuss.php?d=78
Here are more details than in that report, to illustrate the problem and why it arises.
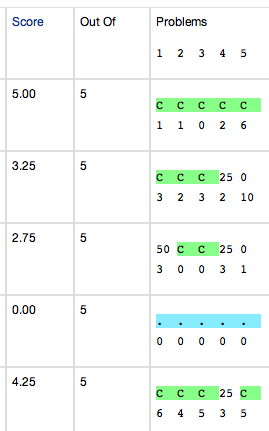
The first column of the screenshot shows homework totals
5.00, 3.25, 2.75, 0.00, 4.25.
5.0, 3.2, 2.8, 0.0, 4.2.
I suggest that in all places where scores are displayed to 1 or 2 decimals (rather than full precision) or in 01-99 format, you change them to consistently use two decimals (never one) and that you round using a consistent method. Preferably floor(100.0*x+.5)/100.0 instead of sprintf("%.2f",x) (or for one decimal, replace 100.0 by 10.0).
The 1 decimal vs. 2 discrepancy is in every problem set. The extent of the rounding halves issue varies by problem set due to which denominators arise in fractional points. It's very likely to happen in a 4 part problem with weight 1 (1 part right and 3 parts wrong gives 0.25 points), but it can also happen in other ways.
Example 2: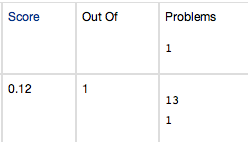
Make a one problem set consisting of this 8-part problem, and assign it a weight of 1:
Library/272/setStewart14_5/problem_3.pg
Enter the correct answer for one part and leave the other parts blank, for a score 0.125. This is both the problem total and the homework total. It is rounded and reported in three unequal ways:
(b) The same screenshot shows the homework total is "0.12" (which uses "round half to even" with 2 decimals).
(c) The homework total in the downloaded score files is "0.1" (which uses "round half to even" with 1 decimal).
Details on rounding methods:
The normal rule of rounding a 5 up is "Round half up". WeBWorK appears to use "Round half to even" for homework totals, which would be explained if you use
sprintf("%.1f",x) or sprintf("%.2f",x) for 1 or 2 decimals.
http://en.wikipedia.org/wiki/Rounding#Round_half_up
http://en.wikipedia.org/wiki/Rounding#Round_half_to_even
Here's a demo to show that they're different. The discrepancies arise due to different rounding methods combined with the fact that some decimal numbers can't be precisely represented in double precision. Similar issues arise when rounding from many decimals to two decimals.
| x | sprintf("%.1f",x) | floor(10.0*x+0.5)/10.0 |
| 0.05 | 0.1 | 0.1 |
| 0.15 | 0.1 | 0.2 (discrepancy) |
| 0.25 | 0.2 | 0.3 (discrepancy) |
| 0.35 | 0.3 | 0.4 (discrepancy) |
| 0.45 | 0.5 | 0.5 |
| 0.55 | 0.6 | 0.6 |
| 0.65 | 0.7 | 0.7 |
| 0.75 | 0.8 | 0.8 |
| 0.85 | 0.8 | 0.9 (discrepancy) |
| 0.95 | 0.9 | 1.0 (discrepancy) |