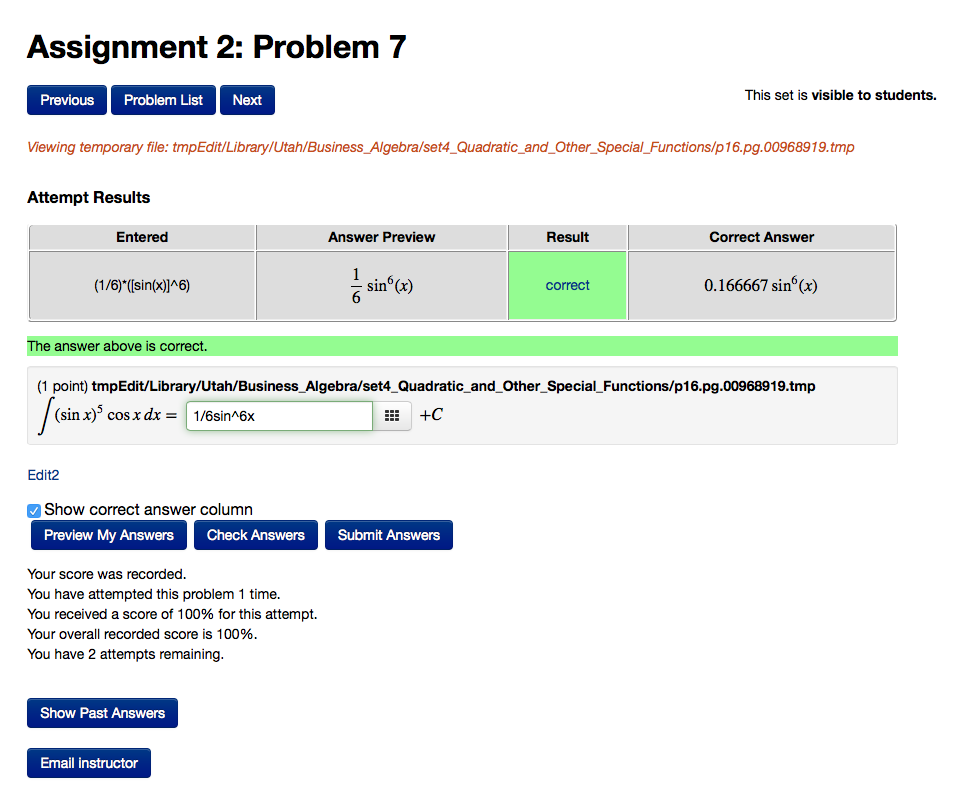
I assigned a trigonometric integral with a random variable, and I was having problems when the answer involved a fraction with infinite digits (in the particular case, 1/6). The integral was the integral of sin^a(x)*cos(x), with an answer of 1/(a+1)*(sin(x))^(a+1). When a is 5, the system seems to round the 1/6 in my answer, and then not recognize a student answer as correct when they put the 1/6 in it. I wonder if the 'upToConstant' has something to do with it...
Here is my code:
DOCUMENT();
loadMacros(
"PGstandard.pl",
"PGML.pl",
"PGcourse.pl"
);
TEXT(beginproblem());
$a = random(3,7,2);
$f = Formula("(sin x)**($a)*(cos x)");
$F = Formula("1/($a+1)*(sin x)**($a+1)");
$ans = $F;
BEGIN_PGML
[`` \int (\sin x)^[$a] \cos x \, dx = ``] [_______________________]{$ans->cmp(upToConstant=>1)} [` +C `]
END_PGML
ENDDOCUMENT;
To temporarily fix the issue, I added the following lines of code after my definition of $a:
if ($a == 5)
{ $a = 7; }
if ($a == 6)
{ $a = 7; }
Thank you for the help.