Hi all,
I'm trying to understand quotes in defining variables using Compute() and how that impacts whether fractions are stored as fractions or six-digit decimal approximations.
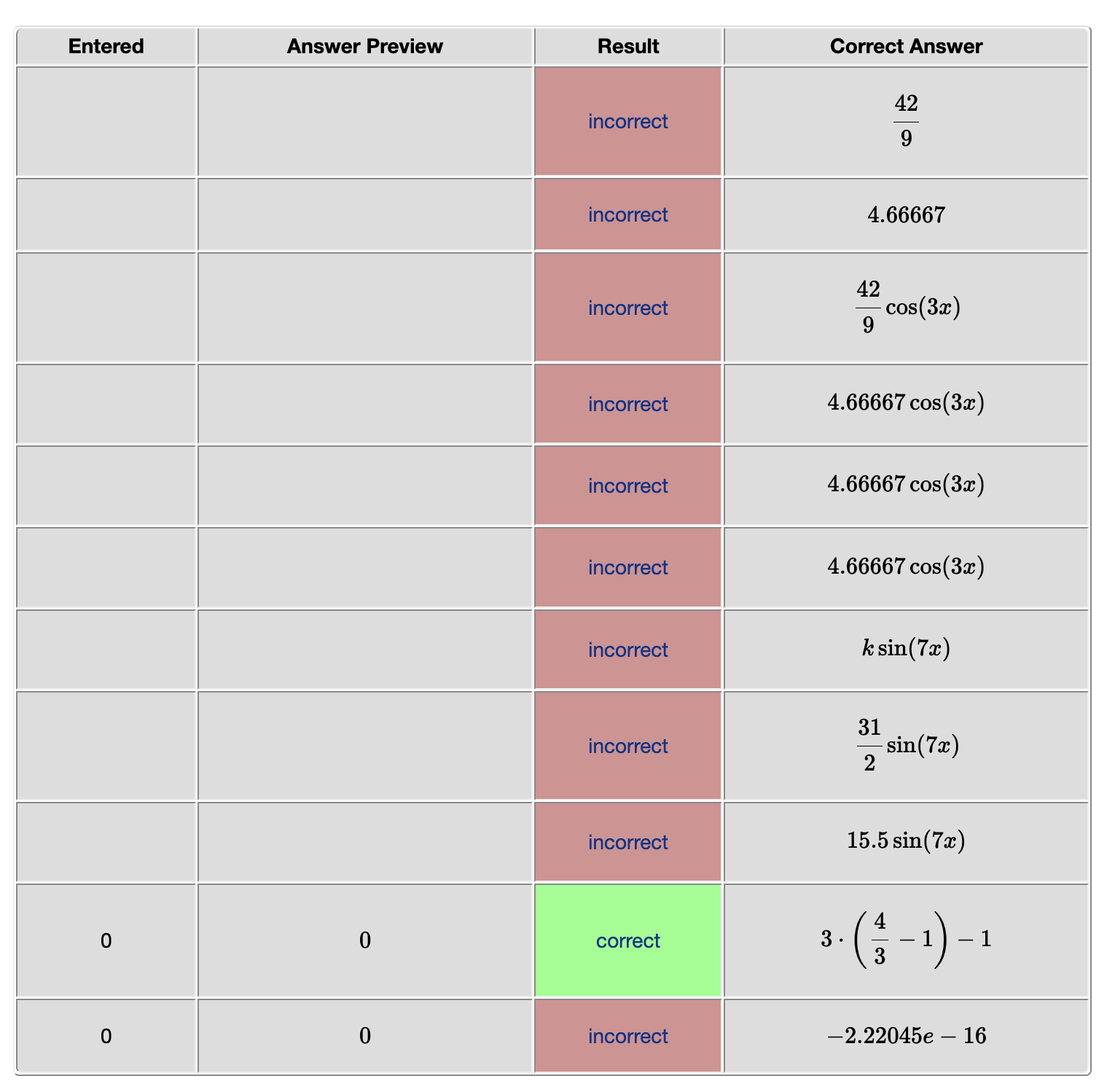
In the MWE below, typing fractions inside quotes seem to result in fractions staying as fractions, but everything else -- products of variables and substituting in to variables doesn't. I'm particularly interested in having $func_subbed keep the fraction, but it doesn't. How do I structure this so that the 42/9 stays 42/9 not 4.66667?
I think I saw a forum post that quotes will force conversion to strings, with attendant decimals, but perhaps I misunderstood that post, as it seems to contradict what I'm seeing here...
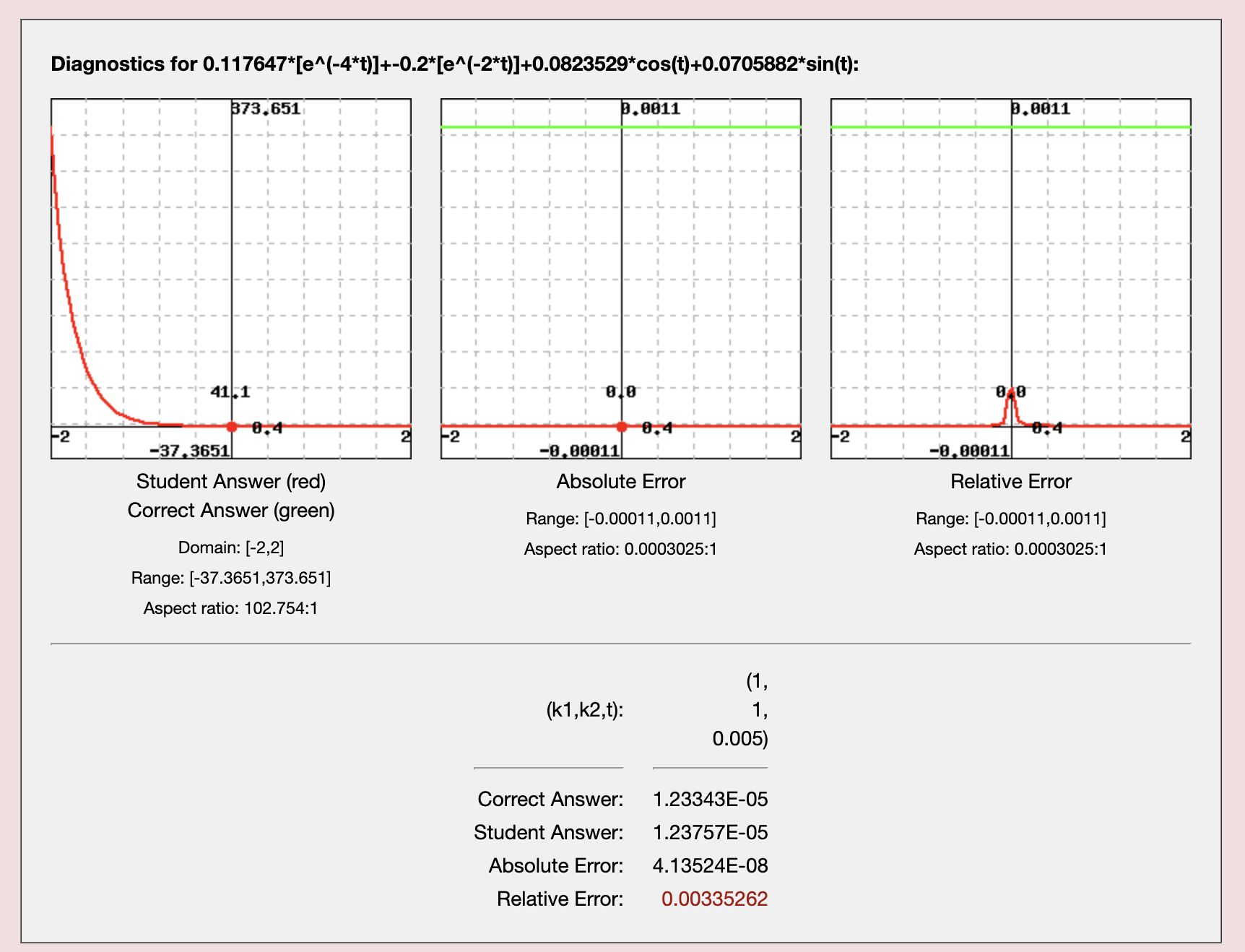
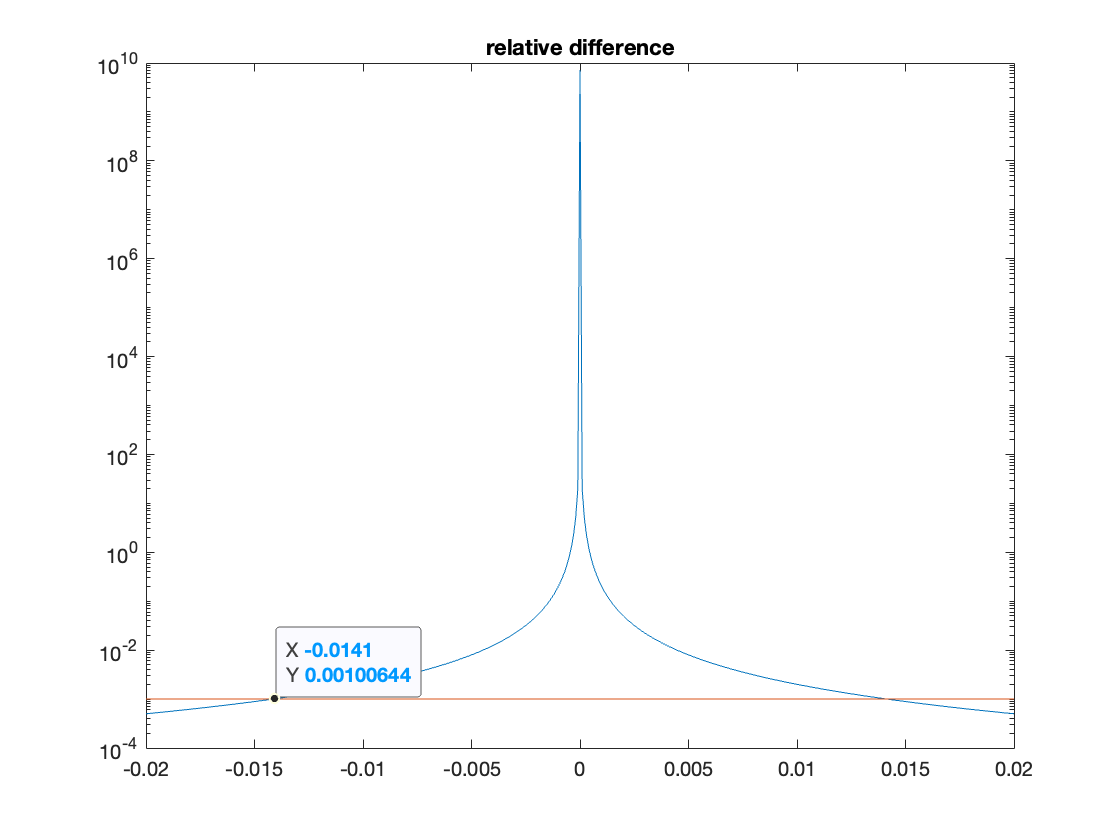
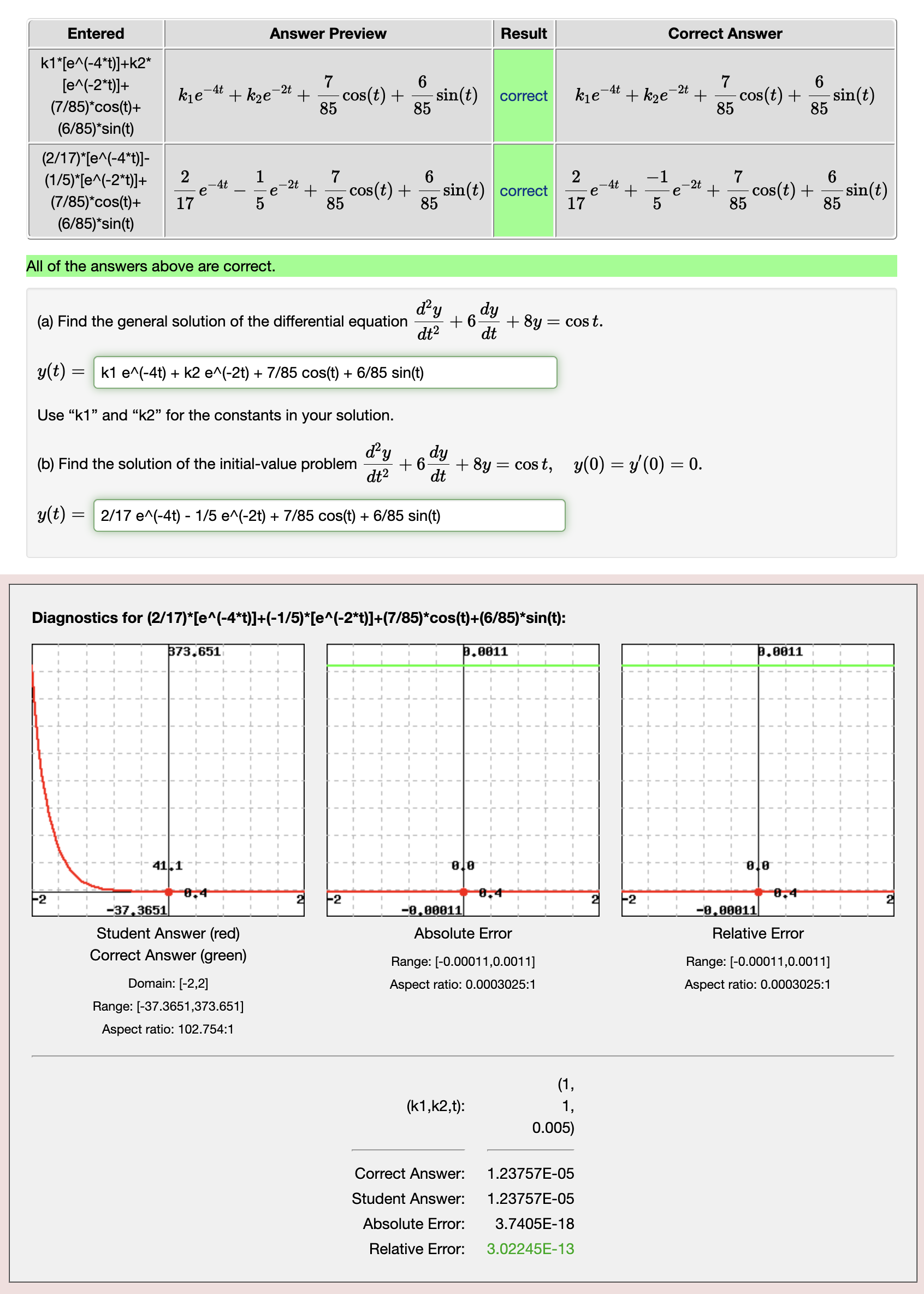
(This came up in a solution to an ODE with initial condition y(0)=0. When a random evaluation point in the answer checker was smaller than about 0.01 in magnitude, having six-decimal approximations for the fractional coefficients of four exponential and sin/cos terms resulted in the value of the webwork correct answer being different from the student's correct answer with fractions -- by greater than the tolerance. Of course setting $ans->limits=[0.5, 2] or increasing the tolerance works, but a more elegant and non-problem-specific solution would be nice.)
((The machine epsilon bit was just for fun...))
Thanks! - Thomas
DOCUMENT();
loadMacros("PGstandard.pl", "PGML.pl", "PGcourse.pl");
Context("Numeric");
$num_quote = Compute("42/9");
$num_noquo = Compute(42/9);
$func_sub = Compute("cos(3x)");
$func_typed = Compute("42/9*cos(3x)");
$func_quote = Compute("$num_quote $func_sub");
$func_noquo = Compute($num_noquo*$func_sub);
$func_perl = $num_quote*$func_sub;
Context()->variables->add(k=>"Real");
$const = Compute("31/2");
$func_const = Compute("k*sin(7x)");
$func_value = Compute("31/2*sin(7x)");
$func_subbed = $func_const->substitute(k=>$const);
$bonus1 = Compute("3(4/3-1)-1"); # just for fun...
$bonus2 = Compute(3*(4/3-1)-1); # as expected
BEGIN_PGML
1. Number with quotes: [_____]{$num_quote}
1. Number no quotes: [_____]{$num_noquo}
1. Function typed out: [____________]{$func_typed}
1. Function with quotes: [____________]{$func_quote}
1. Function no quotes: [____________]{$func_noquo}
1. Function via perl: [____________]{$func_perl}
1. Function with constant: [____________]{$func_const}
1. Function value typed in: [____________]{$func_value}
1. Function value subbed in: [____________]{$func_subbed}
1. 0: [_____]{$bonus1}
1. [`\epsilon`]: [_____]{$bonus2}
END_PGML
ENDDOCUMENT();