I did the Webwork authoring PREP course in the summer of 2015, and have been happily writing a few webwork problems for my students since then (nothing terribly ambitious)! I've just run into a weird little problem that I have no idea how to solve, and I'm hoping someone here can help me.
In a nutshell: there's a number which is being calculated in my code and which should be 10, but which is displaying to the student as 9.99999999999999 instead, which is confusing for the student. However, this problem is occurring only for certain seed values; for other students, the numbers are showing up as integers, as expected.
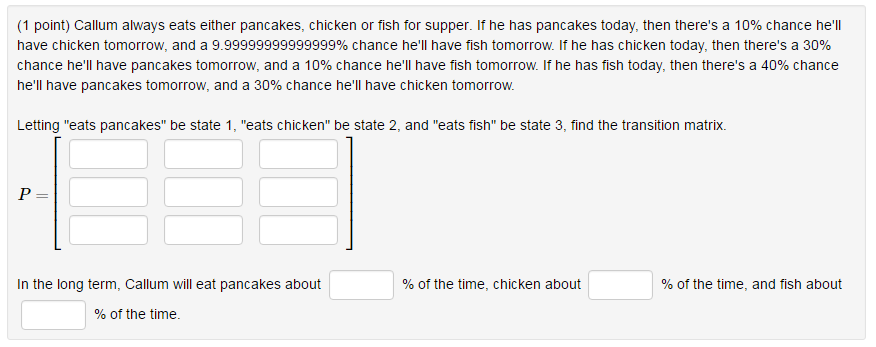
I'm including a code and also a screenshot of the affected student's problem. The seed value for the affected student is 3892. Thanks for any help you can give me!
- Alice McLeod
## Markov chain problem for Linear Algebra (Social Science/Commerce)
## Written by Alice McLeod
DOCUMENT();
loadMacros(
"PGstandard.pl", # Standard macros for PG language
"MathObjects.pl",
"MatrixCheckers.pl",
);
TEXT(beginproblem());
# Show which answers are correct and which ones are incorrect
$showPartialCorrectAnswers = 1;
##############################################################
#
# Setup
#
#
Context("Numeric");
# Generate the transition matrix
do {
$a = random(0.1,0.8,0.1);
$b = random(0.1,0.8,0.1);
} until ($a+$b<1);
$x = 1-$a-$b;
do {
$c = random(0.1,0.8,0.1);
$d = random(0.1,0.8,0.1);
} until ($c+$d<1);
$y = 1-$c-$d;
do {
$e = random(0.1,0.8,0.1);
$f = random(0.1,0.8,0.1);
} until ($e+$f<1);
$z = 1-$e-$f;
Context("Matrix");
$transition = Matrix( [[$a,$c,$e],[$b,$d,$f],[$x,$y,$z]]);
# convert needed probabilities into percent for inclusion in question
Context("Numeric");
Context()->{format}{number} = "%.1f";
$bper = $b*100;
$xper = $x*100;
$cper = $c*100;
$yper = $y*100;
$eper = $e*100;
$fper = $f*100;
# set up steady state vector
$k1 = $e/(1-$a) - ($c/((1-$a)*$y+$c*$x))*(-$e-$f+($e*$x)/(1-$a));
$k2 = -((1-$a)*(-$e-$f)+$e*$x)/($y*(1-$a)+$c*$x);
$t = 1/($k1 + $k2 +1);
$q1 = $t*$k1;
$q2 = $t*$k2;
$q3 = $t;
Context("Matrix");
$q = Matrix([[$q1], [$q2], [$q3]]);
# convert needed probabilites into percent for final answer
Context("Numeric");
# Tolerance set to allows student to round to nearest whole number
$q1per = Compute($q1*100)->with(
tolType => 'absolute',
tolerance => .51,
);
$q2per = Compute($q2*100)->with(
tolType => 'absolute',
tolerance => .51,
);
$q3per = Compute($q3*100)->with(
tolType => 'absolute',
tolerance => .51,
);
##############################################################
#
# Text
#
#
Context()->texStrings;
BEGIN_TEXT
Callum always eats either pancakes, chicken or fish for supper. If he has pancakes today, then there's a $bper$PERCENT chance he'll have chicken tomorrow, and a $xper$PERCENT chance he'll have fish tomorrow. If he has chicken today, then there's a $cper$PERCENT chance he'll have pancakes tomorrow, and a $yper$PERCENT chance he'll have fish tomorrow. If he has fish today, then there's a $eper$PERCENT chance he'll have pancakes tomorrow, and a $fper$PERCENT chance he'll have chicken tomorrow.
$BR
$BR
Letting "eats pancakes" be state 1, "eats chicken" be state 2, and "eats fish" be state 3, find the transition matrix.
$BR
\(P=\)\{$transition->ans_array\}
$BR
$BR
In the long term, Callum will eat pancakes about \{ ans_rule(3) \}$PERCENT of the time, chicken about \{ ans_rule(3) \}$PERCENT of the time, and fish about \{ ans_rule(3) \}$PERCENT of the time.
END_TEXT
Context()->normalStrings;
##############################################################
#
# Answers
#
#
ANS($transition->cmp() );
ANS($q1per->cmp() );
ANS($q2per->cmp() );
ANS($q3per->cmp() );
ENDDOCUMENT();